LN
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NA
1
25 tháng 2 2017
A B C M N
Ta có: \(AB-BM=AC-CN\)
\(\Rightarrow AM=AN\)
\(\Rightarrow\Delta AMN\) cân tại A
\(\Rightarrow\widehat{AMN}=\widehat{ANM}\)
Áp dụng t/c tổng 3 góc trong 1 t/g ta có:
\(\widehat{AMN}+\widehat{ANM}+\widehat{BAC}=180^o\)
\(\Rightarrow\widehat{AMN}=\frac{180^o-\widehat{BAC}}{2}\left(1\right)\)
Do \(\Delta ABC\) cân tại A
\(\Rightarrow\widehat{ABC}=\widehat{ACB}\)
Áp dụng tc tổng 3 góc trong 1 t/g ta có:
\(\widehat{ABC}+\widehat{ACB}+\widehat{BAC}=180^o\)
\(\Rightarrow\widehat{ABC}=\frac{180^o-\widehat{BAC}}{2}\left(2\right)\)
Từ (1) và (2) suy ra \(\widehat{AMN}=\widehat{ABC}\)
mà 2 góc này ở vị trí đồng vị nên \(MN\) // \(BC.\)
27 tháng 2 2017
Cảm ơn bạn nhiều nha. Mà nè sao mk cho là ABC cân rùi mà chứng minh lại làm chi?
1 tháng 7 2016
1 mickey , jerry
2 vịt nào chả đi bằng 2 chân
3 con người
4 hổ ko ăn cỏ
5 tháng nào cũng có
6 tên nam
7 vào quả bóng
8 dùng ống hút
9 1 chữ C
10 nhiều câu ví dụ như cho tao ny mày nhé vvv
11 vất cây thước lấy compa ra vẽ
12 cổ tay phải
13 cái quan tài
14 vì nhắm cả 2 mắt ko bắn được
15 từ chính
16 ba n = bố n = bốn
17 thứ nhì
18 cuối cùng
1 tháng 7 2016
1.chuột túi
3.con người
9.một
12.cổ tay phải
MÌNH CHỈ BIẾT VẬY THÔI
8 tháng 2 2016
Bình không đạt giải nhất, nhì, ba => Bình đạt giải khuyến khích
An không đạt giải nhất, nhì, ba => An đạt giải khuyến khích
Cường không đạt giải nhất, ba, khuyến khích => Cường đạt giải nhì
Đông không đạt giải nhất, ba khuyến khích => Đông đạt giải nhì
15 tháng 11 2015
Không phải khi sai à ?
Vậy có lẽ khi làm không đúng !!!!!!
NT
29 tháng 12 2017
a)
Xét \(\Delta ANM;\Delta CNE\) có :
\(AN=NC\left(gt\right)\\ \widehat{ANM}=\widehat{CNE}\left(đ^2\right)\\ NM=NE\left(gt\right)\\ \Rightarrow\Delta ANM=\Delta CNE\left(c-g-c\right)\\ \Rightarrow AM=CE;\widehat{A}=\widehat{NCE}\)
AM=CE => BM=CE
\(\widehat{A}=\widehat{NCE}\\ \)
=> CE // AB
=> CE // MB
b)
Xét \(\Delta ANE;\Delta CNM\) có :
\(NA=NC\left(gt\right)\\ \widehat{ANE}=\widehat{CNM}\left(đ^2\right)\\ NE=NM\left(gt\right)\\ \Rightarrow\Delta ANE=\Delta CNM\left(c-g-c\right)\\ \Rightarrow AE=CM\)
\(AB=AC\\ \Rightarrow\dfrac{AB}{2}=\dfrac{AC}{2}\\ \Rightarrow BM=CN\)
Xét \(\Delta BCM;\Delta CBN\) có :
\(BM=CN\left(gt\right)\\ \widehat{ABC}=\widehat{ACB}\left(gt\right)\\ BC\left(chung\right)\\ \Rightarrow\Delta BCM=\Delta CBN\left(c-g-c\right)\\ \Rightarrow MC=BN\)
Xét tam giác ADC ; B là trung điểm AD ; N là trung điểm AC
=> BN là đường trung bình tam giác ADC
\(\Rightarrow BN=\dfrac{1}{2}CD\\ \Rightarrow AE=\dfrac{CD}{2}\)
CM
25 tháng 10 2019
Ta có : 4cm + 3cm = 7cm > 6cm.
⇒ Bộ ba đoạn thẳng 3cm, 4cm, 6cm thỏa mãn bất đẳng thức tam giác nên là ba cạnh của tam giác.
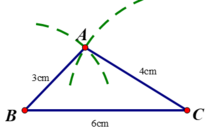
Cách dựng tam giác có ba độ dài 3cm, 4cm, 6cm
- Vẽ BC = 6cm
- Dựng đường tròn tâm B bán kính 3cm ; đường tròn tâm C bán kính 4cm. Hai đường tròn cắt nhau tại A. Nối AB, AC ta được tam giác cần dựng.
Bố là ba (nghĩa là cha đó) nên ba n= Bố n= bốn \(\ne\) bốn n nên đề sai