Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

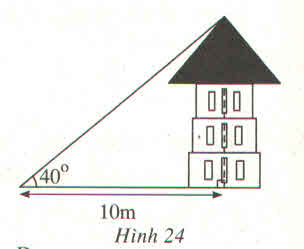
a. Chiều cao tòa nhà là cạnh góc vuông đối diện với góc 40o, khoảng cách từ chỗ người trinh sát đứng đến ngôi nhà là cạnh kề.
Chiều cao của tòa nhà là:
10.tg40o ≈ 8,391 (m)
b. Nếu dịch chuyển sao cho góc “nâng” là 35o thì anh ta cách tòa nhà:
8,391.cotg35o ≈ 11,934 (m)

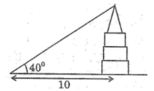
Chiều cao tòa nhà là cạnh góc vuông đối diện với góc 40 ° , khoảng cách từ chỗ người trinh sát đứng đến ngôi nhà là cạnh kề.
Chiều cao của tòa nhà là:
10.tg 40 ° ≈ 8,391 (m)

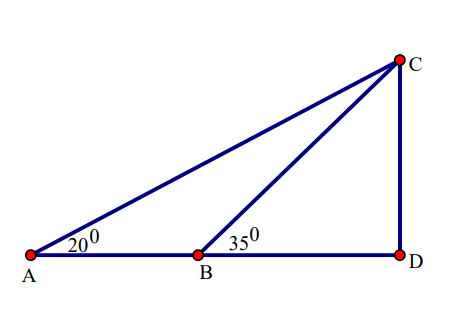
Hai vị trí cách nhau 12m tức là \(AB=12\left(m\right)\)
Ta có \(\tan\widehat{A}=\dfrac{CD}{AD}=\tan20^0\approx0,4\Leftrightarrow AD=\dfrac{CD}{0,4}\)
\(\tan\widehat{CBD}=\dfrac{CD}{BD}=\tan35^0\approx0,7\Leftrightarrow BD\approx\dfrac{CD}{0,7}\)
Ta có \(AD-BD=AB=12\)
\(\Leftrightarrow\dfrac{CD}{0,4}-\dfrac{CD}{0,7}=12\Leftrightarrow CD=\dfrac{56}{5}=11,2\left(m\right)\)
Vậy...

Nếu dịch chuyển sao cho góc “nâng” là 35 ° thì anh ta cách tòa nhà:
8,391.cotg 35 ° ≈ 11,934 (m)

Tòa nhà cao \(24\cdot4=96\left(m\right)\)
Tia nắng hợp với tòa nhà 1 góc \(\tan^{-1}\left(\dfrac{20}{24}\right)\approx40^0\)
A B C D 30 65 20
xét tg vuông ABC có:
tan B=AC/BC
suy ra BC=AB/tan B
xét tg vuông DAC có:
tan D=AC/BD
suy ra BD=AC/tan D
theo đề bài ta có pt:
BD+20=BC
(AC/tan D)+20=(AC/tan B)
(AC/tan 65)+20=(AC/tan 30) gần = 15.8
chiều cao của toà nhà là:
15.8+1.5 gần = 17.3(m)
vậy chiều cao của toà nhà khoảng 17.3 m