Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C
Phương pháp: Lập hàm số chi phí theo một ẩn sau đó tìm giá trị nhỏ nhất của hàm số đó.
Cách giải: Gọi a là chiều dài cạnh đáy hình vuông của hình hộp chữ nhật và b là chiều cao của hình hộp chữ nhật ta có a 2 b = 8 a , b > 0 ⇒ a b = 8 a
Diện tích đáy hình hộp là a 2 và diện tích xung quanh là 4ab nên chi phí để làm thùng tôn là 100 a 2 + 50.4 a b = 100 a 2 + 200 a b = 100 a 2 = 100. 8 a = 100 a 2 + 1600 a = 100 a 2 + 16 a
Áp dụng BĐT Cauchy ta có a 2 + 16 a = a 2 + 8 a + 8 a ≥ 3 a 2 + 8 a + 8 a 3 = 3.4 = 12
Dấu bằng xảy ra khi và chỉ khi a 2 + 8 a ⇔ a = 2.
Vậy chi phí nhỏ nhất bằng 1200000 đồng khi và chỉ khi cạnh đáy hình hộp bằng 2m.

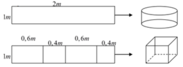
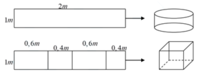
Gọi chiều dài tấm tôn là x (cm) (0 < x < 60) Suy ra chiều rộng: 60 - x (cm)
Giả sử quấn tấm tôn theo cạnh có kích thước x => bán kính đáy r = x 2 π và chiều cao h = 60 - x
Khi đó
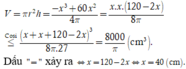
Chọn C.

Chọn A
Phương pháp: Sử dụng công thức thể tích hình trụ và công thức thể tích hình hộp.
Cách giải:


Đáp án A.
Gọi cạnh đáy của khối chóp là x với
0 < x < 5 2 2 .
Chiều cao của khối chóp là
h = 5 2 2 − x 2 2 − x 2 2 = 25 − 5 x 2 2 .
Vậy thể tích của khối chóp là
V = 1 3 . h . S = 1 3 . x 2 . 25 − 5 x 2 2 = 1 3 25 x 4 − 5 x 5 2 2 .
Xét hàm số f x = 25 x 4 − 5 x 5 2 trên 0 ; 5 2 2 ,
ta có f ' x = 100 x 3 − 25 x 4 2 = 0 ⇔ x = 2 2 .
Suy ra giá trị lớn nhất của thể tích là V = 1 3 . f 2 2 2 = 4 10 3 .
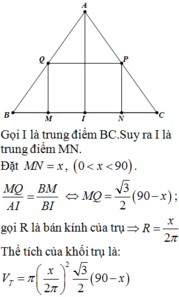
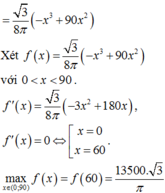
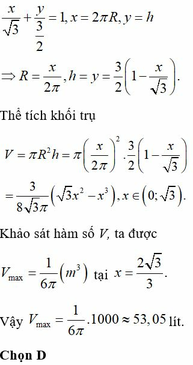
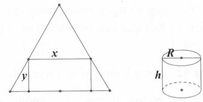
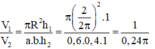

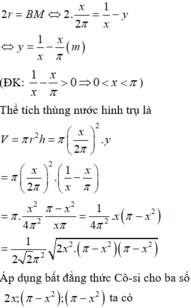
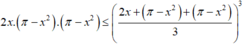
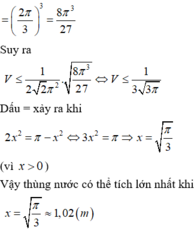
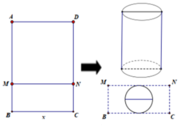

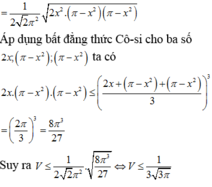
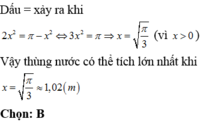
Chọn đáp án D.