Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Mk sẽ giúp bạn
a) 70 . 2 + 21 . 3 + 15 . 4 + (-) 105k = 263 + (-) 105k ( k thuộc N )
b) Gọi số quân là n
n = 3x + a => 70n = 210x + 70a
n = 5y + b => 21n = 105y + 21b
n = 7z + c => 15n = 105z + 15c
Do đó : 106n = 70a + 21b + 15c + (-) 105t
Vậy n = 70a + 21b + 10c + (-) 105h
Duyệt đi bạn nhé

a) Số học sinh tham dự giải Lương Thế Vinh là:
70.2 + 21.3 + 15.4 + 105m \(\left(m\in N\right)\)= 263 + 105m
Theo đầu bài, ta có: \(4600\le263+105m\le4700\)
\(4337\le105m\le4367\)
\(4337>105.41;4367< 105.43\)
Do đó 41 < m < 43 nên m = 42
Vậy số học sinh tham dự giải Lương Thế Vinh là:
263 + 105.42 = 4673 (học sinh)
b) Gọi số quân là x
Ta có: \(x-a⋮3\Rightarrow70x-70\text{a}⋮105\)
\(x-b⋮5\Rightarrow21\text{x}-21b⋮105\)
\(x-c⋮7\Rightarrow15\text{x}-15c⋮105\)
Do đó \(\left(70\text{x}+21\text{x}+15\text{x}\right)-\left(70\text{a}+21b+15c\right)⋮105\)
\(106x-\left(70\text{a}+21b+15c\right)⋮105\)
Vậy \(x=70\text{a}+15b+21c\pm b\text{ội}105\)

Tục truyền rằng ngày xưa, Hàn Tín danh tướng của Hán Cao tổ dùng phép sau này để điểm binh:
Bảo lính sắp hàng ba hàng năm và hàng bảy, rồi đếm hàng lẻ cuối cùng. Ghi những số lẻ ấy.
Nhân số lẻ hàng ba cho 70, số lẻ hàng năm cho 21 và số lẻ hàng bảy cho 15, rồi cộng lại.
Lấy số thành mà thêm bớt một bội số của 105 thì được số lính.
Ví dụ sắp hàng ba lẻ 2; sắp hàng năm lẻ 3 và sắp hàng bảy lẻ 4. Theo phép trên thì số lính là:
N = (2 x 70) + (3 x 21) + (4 x 15) + k.105 hay là
N = 263 + k.105 k là một số nguyên, âm dương tùy đó, to nhỏ tùy đó.
Muốn biết số N một cách chính xác thì phải biết chừng N trong khoảng 105 hoặc ít hơn.
Như N chừng từ 800 đến 900 thì k là 6 và N = 263 + (6 x 105) hay là N = 893
*NGUỒN GỐC CỦA QUY TẮC HÀN TÍN:
Bài toán trên đây, ta có thể đặt như thế này:
Một số S chia cho 3 còn a, chia cho 5 còn b, chia cho 7 còn c. Vậy chia cho 3 x 5 x 7 hoặc 105 còn bao nhiêu?
Ta có thể viết theo ba phép chia như sau:
S = 3.A + a
S = 5.B + b
S = 7.C + c
a, b, c lần lượt kém 3, 5, 7 và cũng có thể là số không.
Ta nhân hai vế đẳng thức đầu với 5.7.m ; được: 35.m.S = 105.m.A + 35.m.a
Ta nhân hai vế đẳng thức thứ hai với 7.3.n; được: 21.n.S = 105.n.B + 21.n.b
Ta nhân hai vế đẳng thức thứ ba với 3.5.p; được: 15.p.S = 105.p.C + 15.p.c
Cộng ba đẳng thức mới được lại. Thành:
(1) (35m + 21n + 15p). S = 105.(mA + nB + pC) + 35ma + 21nb + 15pc
Ta sẽ tìm ba số nguyên m, n, p nghiệm đẳng thức sau đây:
(2) 35m + 21n + 15p = 105k + 1
Ta viết (2) như sau: 35m - 1 = 3(35k - 7n - 5p)
=> 36m -(m+1) = 3(35k - 7n - 5p)
=> m+1 chia hết cho 3
=> m = 2 + 3M
Ta quay trở lại đẳng thức (2) mà ứng dụng lý luận vừa dùng để kiếm n rồi kiếm p. Ta sẽ thấy:
21n - 1 = 5.(21k - 7m - 3p)
20n + (n-1) = (21k - 7m - 3p)
=> n- 1 chia hết cho 5
=> n = 1 + 5N
Tương tự
35m + 21n + 15p = 105k + 1
=> 15p - 1 = 7(15k -5m -3n)
=> 14p + p-1 = 7(15k -5m -3n)
=> p + 1 chia hết cho 7
=> p có dạng
=> p = 1 + 7P
Làm như thế, ta được vô số những số m, n, p nghiệm đẳng thức (2).
Ta lấy ba số M = N = P = 0, ta được ba số: m = 2, n = 1, p = 1 gọn nhất.
Thay nó vào đẳng thức (1) ta sẽ thấy:
(105 + 1).S = 105.(2A + B + C) + 70a + 21b + 15c
Hay là: S = 105.T + (70a + 21b + 15c)
Vậy số S bằng 70a + 21b + 15c rồi thêm bớt một bội số của 105.
Tục truyền rằng ngày xưa, Hàn Tín danh tướng của Hán Cao tổ dùng phép sau này để điểm binh:
Bảo lính sắp hàng ba hàng năm và hàng bảy, rồi đếm hàng lẻ cuối cùng. Ghi những số lẻ ấy.
Nhân số lẻ hàng ba cho 70, số lẻ hàng năm cho 21 và số lẻ hàng bảy cho 15, rồi cộng lại.
Lấy số thành mà thêm bớt một bội số của 105 thì được số lính.
Ví dụ sắp hàng ba lẻ 2; sắp hàng năm lẻ 3 và sắp hàng bảy lẻ 4. Theo phép trên thì số lính là:
N = (2 x 70) + (3 x 21) + (4 x 15) + k.105 hay là
N = 263 + k.105 k là một số nguyên, âm dương tùy đó, to nhỏ tùy đó.
Muốn biết số N một cách chính xác thì phải biết chừng N trong khoảng 105 hoặc ít hơn.
Như N chừng từ 800 đến 900 thì k là 6 và N = 263 + (6 x 105) hay là N = 893

gọi số kiến là a(a thuộc N)
ta có:
a chia hết cho 3;5;7=>a thuộc BC(3;5;7)
3=3;5=5;7=7
=>BCNN(3;5;7)=3.5.7=105
=>a thuộc B(105)
vì a bé hơn 200 và a khác 0 nên a=105
vậy số kiến là 105.
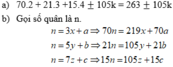
b)
Gọi số quân là n
n=3x+a => 70n=219x+70a
n=5y+b => 21n=105y+21b
n=7z+c => 15n=105z+15c
Do đó: 106n = 70a +21b + 15c ± 105t (t ∈N)
Vậy n = 70a + 21b + 10c ± 105h (h ∈N)