Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bài 1 : biến x^4y^3tz^4
Bài 2 :
Theo bài ra ta có a > 0
cạnh còn lại là 2a
Theo định lí Pytago \(a^2+2a^2=3a^2\)
Vậy bình phương cạnh huyền là 3a^2
1) Phần biến của đơn thức đã cho là \(xy^3xtz^4x^2\)
2) Độ dài cạnh góc vuông còn lại là \(2a\)
Theo định lý Py-ta-go, ta có bình phương cạnh huyền bằng \(a^2+\left(2a\right)^2=a^2+4a^2=5a^2\)
3) \(4mx^{2n+5}y^{m-1}=\left(\frac{4}{3}x^ny^3\right).\left(3mx^{n+5}y^{m-4}\right)\)

a: \(=2x^5\cdot2y^{12}\cdot4z^8\)
b: \(=4x^5y^{12}z^8+4x^5y^{12}z^8+5x^5y^{12}z^8+3x^5y^{12}z^8\)

Ta có:8xa9xb6=23x(a3)3x(b2)3=(2xa3xb2)3
k mình nha mình k lại cho

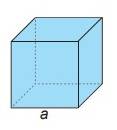
Công thức tính thể tích hình lập phương cạnh a là:
V= a.a.a = \({a^3}\)
Bài toán mở đầu:
Biểu thức lũy thừa tính toàn bộ lượng nước trên Trái Đất trong bài toán mở đầu (đơn vị kilomét khối) là:
V =\({(1111,34)^3}\)

Đơn thức cần tìm là A thì ta có -3x2y = 2x2y + A
=> A = -3x2y - 2x2y = -5x2y (cách cộng hai đơn thức là: ta cộng phần hệ số với nhau và giữ nguyên phần biến)
vậy đơn thức đồng dạng với nó có hệ số bằng -5

GỌI ĐƠN THỨC PHẢI TÌM LÀ\(ax^py^q\left(p,q\in N\right)\)
ta có \(3x^{n+3}y^{m-2}=\frac{2}{5}x^ny^2.ax^py^q;3x^{n+3}y^{m-2}=\frac{2}{5}ax^{n+p}y^{2+q}\)
suy ra \(3=\frac{2}{5}a\Rightarrow a=3:\frac{2}{5}=\frac{15}{2}=7\frac{1}{2}\)
\(n+3=n+p\)
\(\Rightarrow p=3\)
\(m-2=2+q\)
\(\Rightarrow q=m-2-2=m-4\left(q\in n,vớim\in N,m>4\right)\)
vậy đơn thức cần tìm là\(7\frac{1}{2}x^3y^{m-4}\)và ta có\(3x^{n+3}y^{m-2}=\frac{2}{5}x^ny^2.7\frac{1}{2}x^3y^{m-4}\)
a) (4x)2 , (9x2y)2 ,
b) (3ab4)3 , (\(-\frac{1}{5}\)x3y2)