Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

`a)Đặt \, A=sqrt{21+3sqrt{48}}-sqrt{21-3sqrt{48}}`
Vì `21+3sqrt{48}>21-3sqrt{48}`
`=>sqrt{21+3sqrt{48}}-sqrt{21-3sqrt{48}}>0`
Hay `A>0`
`<=>A^2=21+3sqrt{48}+21-3sqrt{48}-2sqrt{21^2-9.48}`
`<=>A^2=42-2sqrt{9}=32-2.3=26`
`<=>A=sqrt{26}(do \ A>0)`
b)Chắc đề là như này:
`sqrt{7-2sqrt{10}}-sqrt{7+2sqrt{10}}`
`=sqrt{5-2sqrt{5}.sqrt2+2}-sqrt{5+2sqrt{5}.sqrt2+2}`
`=sqrt{(sqrt5-sqrt2)^2}-sqrt{(sqrt5+sqrt2)^2}`
`=sqrt5-sqrt2-sqrt5-sqrt2=-2sqrt2`

\(1,\)
\(a,\sqrt{6-2\sqrt{5}}=\sqrt{\sqrt{5^2}-2.\sqrt{5}.1+1}=\sqrt{\left(\sqrt{5}-1\right)^2}=\left|\sqrt{5}-1\right|=\sqrt{5}-1\)
\(b,\sqrt{8+2\sqrt{7}}=\sqrt{\sqrt{7^2}+2.\sqrt{7}.1+1}=\sqrt{\left(\sqrt{7}+1\right)^2}=\left|\sqrt{7}+1\right|=\sqrt{7}+1\)
\(2,\)
\(a,\sqrt{\left(\sqrt{10}-3\right)^2}-\sqrt{10}\)
\(=\left|\sqrt{10}-3\right|-\sqrt{10}\)
\(=\sqrt{10}-\sqrt{10}-3\)
\(=-3\)
\(b,\sqrt{\left(5+\sqrt{7}\right)^2}-\sqrt{8-2\sqrt{7}}\)
\(=\left|5+\sqrt{7}\right|-\sqrt{\left(\sqrt{7}-1\right)^2}\)
\(=5+\sqrt{7}-\left|\sqrt{7}-1\right|\)
\(=5+\sqrt{7}-\sqrt{7}+1\)
\(=6\)

i: =-12*căn 3/2căn 3=-6
h: =72căn 2/12căn 2=6
g: =25căn 12/5căn 6=5căn 2
f: =(15:5)*căn 6:3=3căn 2
d: =-1/2*6*căn 10=-3căn 10

a) \(A=\sqrt{4-2\sqrt{3}}-\sqrt{4+2\sqrt{3}}\)
\(=\sqrt{\left(\sqrt{3}\right)^2-2.\sqrt{3}.1+1^2}-\sqrt{\left(\sqrt{3}\right)^2+2.\sqrt{3}.1+1^2}\)
\(=\sqrt{\left(\sqrt{3}-1\right)^2}-\sqrt{\left(\sqrt{3}+1\right)^2}=\left|\sqrt{3}-1\right|-\left|\sqrt{3}+1\right|\)
\(=\sqrt{3}-1+-\sqrt{3}-1=-2\)
b) \(B=\sqrt{11-6\sqrt{2}}-\sqrt{3-2\sqrt{2}}\)
\(=\sqrt{3^2-2.3.\sqrt{2}+\left(\sqrt{2}\right)^2}-\sqrt{\left(\sqrt{2}\right)^2-2.\sqrt{2}.1+1^2}\)
\(=\sqrt{\left(3-\sqrt{2}\right)^2}-\sqrt{\left(\sqrt{2}-1\right)^2}=\left|3-\sqrt{2}\right|-\left|\sqrt{2}-1\right|\)
\(=3-\sqrt{2}-\sqrt{2}+1=4-2\sqrt{2}\)
c) \(C=\left(\sqrt{3}+\sqrt{5}\right)\sqrt{7-2\sqrt{10}}\)
\(=\left(\sqrt{5}+\sqrt{3}\right)\sqrt{\left(\sqrt{5}\right)^2-2.\sqrt{5}.\sqrt{2}+\left(\sqrt{2}\right)^2}\)
\(=\left(\sqrt{5}+\sqrt{3}\right)\sqrt{\left(\sqrt{5}-\sqrt{2}\right)^2}=\left(\sqrt{5}+\sqrt{3}\right)\left|\sqrt{5}-\sqrt{2}\right|\)
\(=\left(\sqrt{5}+\sqrt{3}\right)\left(\sqrt{5}-\sqrt{2}\right)=5-\sqrt{10}+\sqrt{15}-\sqrt{6}\)

`a)((sqrt(14)-sqrt7)/(1-sqrt2)+(sqrt{15}-sqrt5)/(1-sqrt3)):1/(sqrt7-sqrt5)`
`=((sqrt7(sqrt2-1))/(1-sqrt2)+(sqrt5(sqrt3-1))/(1-sqrt3)).(sqrt7-sqrt5)`
`=(-sqrt7-sqrt5)*(sqrt7-sqrt5)`
`=-(sqrt7+sqrt5)(sqrt7+sqrt5)`
`=-(7-5)=-2`
`b)sqrt2+1/sqrt{5+2sqrt6}+2/sqrt{8+2sqrt{15}}`
`=sqrt2+1/sqrt{3+2sqrt{3}.sqrt2+2}+2/sqrt{5+2sqrt{5}.sqrt3+3}`
`=sqrt2+1/sqrt{(sqrt3+sqrt2)^2}+2/sqrt{(sqrt5+sqrt3)^2}`
`=sqrt2+1/(sqrt3+sqrt2)+2/(sqrt5+sqrt3)`
`=sqrt2+((sqrt3+sqrt2)(sqrt3-sqrt2))/(sqrt3+sqrt2)+((sqrt5+sqrt3)(sqrt5-sqrt3))/(sqrt5+sqrt3)`
`=sqrt2+sqrt3-sqrt2+sqrt5-sqrt3=sqrt5`
a) Ta có: \(\left(\dfrac{\sqrt{14}-\sqrt{7}}{1-\sqrt{2}}+\dfrac{\sqrt{15}-\sqrt{5}}{1-\sqrt{3}}\right):\dfrac{1}{\sqrt{7}-\sqrt{5}}\)
\(=\left(-\dfrac{\sqrt{7}\left(1-\sqrt{2}\right)}{1-\sqrt{2}}-\dfrac{\sqrt{5}\left(1-\sqrt{3}\right)}{1-\sqrt{3}}\right):\dfrac{1}{\sqrt{7}-\sqrt{5}}\)
\(=-2\)
b) Ta có: \(\sqrt{2}+\dfrac{1}{\sqrt{5+2\sqrt{6}}}+\dfrac{2}{\sqrt{8+2\sqrt{15}}}\)
\(=\sqrt{2}+\dfrac{1}{\sqrt{3}+\sqrt{2}}+\dfrac{2}{\sqrt{5}+\sqrt{3}}\)
\(=\sqrt{2}+\sqrt{3}-\sqrt{2}+\sqrt{5}-\sqrt{3}\)
\(=\sqrt{5}\)

\(a,=\dfrac{x^4\left(x-2\right)+2x^2\left(x-2\right)-3\left(x-2\right)}{x+4}\\ =\dfrac{\left(x-2\right)\left(x^4+2x^2-3\right)}{x+4}\\ =\dfrac{\left(x-2\right)\left(x^4-x^2+3x^2-3\right)}{x+4}\\ =\dfrac{\left(x-2\right)\left(x-1\right)\left(x^2+3\right)}{x+4}\)
\(b,=\dfrac{x^4-3x^2-x^2+3}{x^4-x^2+7x^2-7}=\dfrac{\left(x^2-3\right)\left(x^2-1\right)}{\left(x^2+7\right)\left(x^2-1\right)}=\dfrac{x^2-3}{x^2+7}\\ c,=\dfrac{\left(x^3-1\right)\left(x+1\right)}{x^2\left(x^2+x+1\right)+\left(x^2+x+1\right)}\\ =\dfrac{\left(x-1\right)\left(x^2+x+1\right)\left(x+1\right)}{\left(x^2+1\right)\left(x^2+x+1\right)}=\dfrac{x^2-1}{x^2+1}\)

\(1,\\ a,=\sqrt{\left(3+\sqrt{7}\right)^2}-\sqrt{\left(\sqrt{7}-1\right)^2}=3+\sqrt{7}-\sqrt{7}+1=4\\ b,K=\dfrac{\sqrt{\left(\sqrt{3}-1\right)^2}}{\sqrt{2}\left(\sqrt{3}-1\right)}=\dfrac{\sqrt{3}-1}{\sqrt{2}\left(\sqrt{3}-1\right)}=\dfrac{1}{\sqrt{2}}=\dfrac{\sqrt{2}}{2}\\ c,=\sqrt{\left(6-2\sqrt{6}\right)^2}+\sqrt{\left(2\sqrt{6}-4\right)^2}=6-2\sqrt{6}+2\sqrt{6}-4=2\\ e,=\sqrt{\left(2-\sqrt{2}\right)^2}-\left(\sqrt{6}-\sqrt{2}\right)=2-\sqrt{2}-\sqrt{6}+\sqrt{2}=2-\sqrt{6}\)
\(2,\\ a,A=\dfrac{x-3\sqrt{x}+3\sqrt{x}+9}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}\cdot\dfrac{\sqrt{x}+3}{x+9}\\ A=\dfrac{x+9}{\left(\sqrt{x}-3\right)\left(x+9\right)}=\dfrac{1}{\sqrt{x}-3}\\ b,x=4+2\sqrt{3}\Leftrightarrow\sqrt{x}=\sqrt{3}+1\\ \Leftrightarrow A=\dfrac{1}{\sqrt{3}+1-3}=\dfrac{1}{\sqrt{3}+2}=2-\sqrt{3}\)

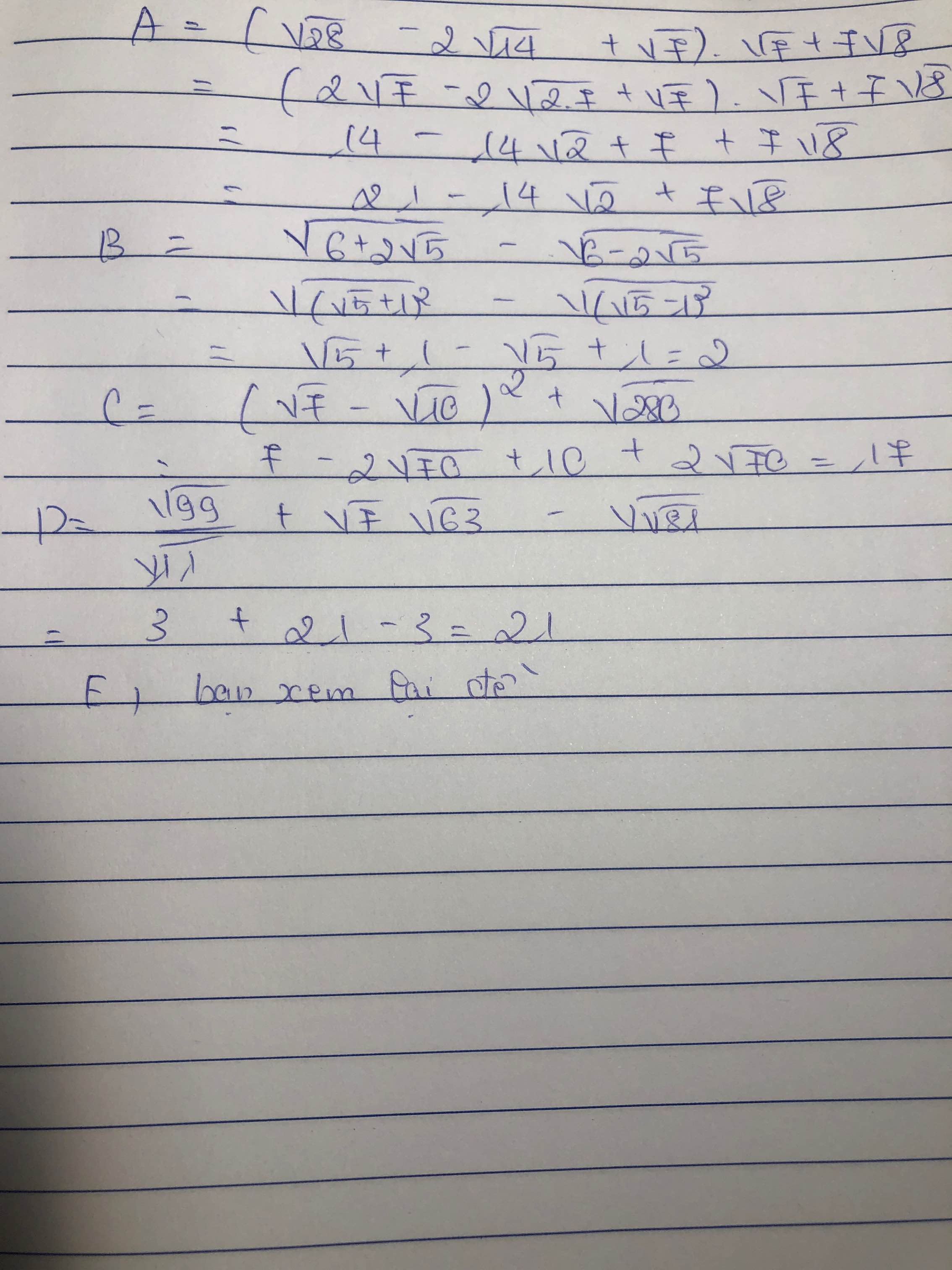
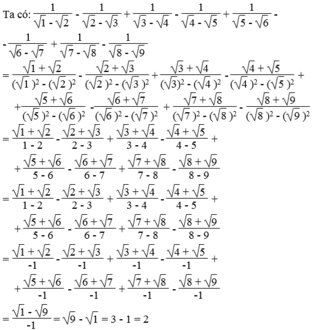
`a)sqrt{8-2sqrt7}+sqrt{16-6sqrt7}`
`=sqrt{(sqrt7-1)^2}+sqrt{(3-sqrt7)^2}`
`=sqrt7-1+3-sqrt7=2`
`b)sqrt{(sqrt7-1)^2}-sqrt{11+4sqrt7}`
`=sqrt7-1-sqrt{(2+sqrt7)^2}`
`=sqrt7-1-2-sqrt7=-3`
a, \(=\sqrt{7-2\sqrt{7}+1}+\sqrt{7-2.3\sqrt{7}+9}\)
\(=\sqrt{\left(\sqrt{7}-1\right)^2}+\sqrt{\left(3-\sqrt{7}\right)^2}=\left|\sqrt{7}-1\right|+\left|3-\sqrt{7}\right|\)
\(=\sqrt{7}-1+3-\sqrt{7}=2\)
\(b,=\left|\sqrt{7}-1\right|-\sqrt{7+2.2\sqrt{7}+4}\)
\(=\left|\sqrt{7}-1\right|-\sqrt{\left(\sqrt{7}+2\right)^2}=\left|\sqrt{7}-1\right|-\left|\sqrt{7}+2\right|\)
\(=\sqrt{7}-1-\sqrt{7}-2=-3\)