
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



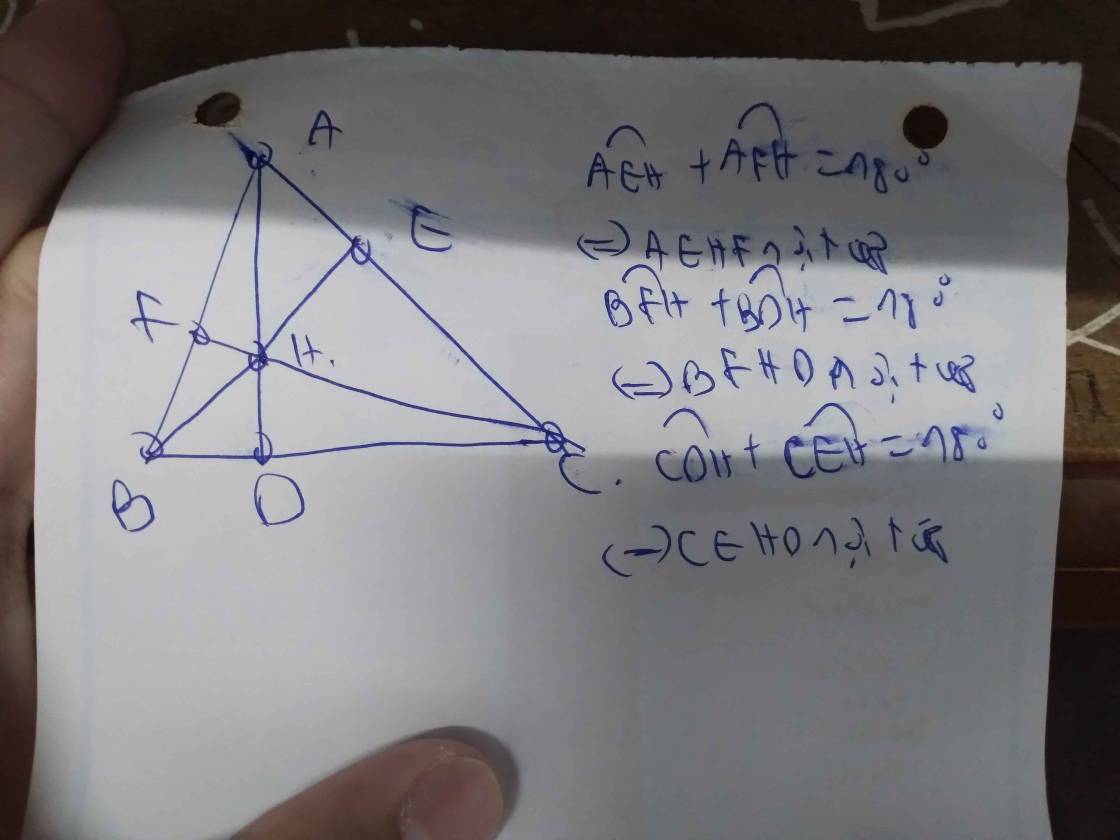
a: Xét tứ giác AEHF có
góc AEH+góc AFH=180 độ
=>AEHF là tứ giác nội tiếp
Xét tứ giác BFEC có
góc BFC=góc BEC=90 độ
=>BFEC là tứ giác nội tiếp
b: Xét (O) có
ΔABK nội tiếp
AK là đường kính
=>ΔABK vuông tại B
=>BK//CH
Xét (O) có
ΔACK nội tiếp
AK là đường kính
=>ΔACK vuông tại C
=>CK//BH
Xét tứ giác BHCK có
BH//CK
BK//CH
=>BHCK là hình bình hành
=>BC cắt HK tại trung điểm của mỗi đường
=>I là trung điểm của BC

a: Xét tứ giác AEHF có
\(\widehat{AEH}+\widehat{AFH}=180^0\)
Do đó: AEHF là tứ giác nội tiép
b: Xét tứ giác ABDE có
\(\widehat{AEB}=\widehat{ADB}=90^0\)
Do đó:ABDE là tứ giác nội tiếp

a) Xét tứ giác BEHD có
\(\widehat{BEH}\) và \(\widehat{BDH}\) là hai góc đối
\(\widehat{BEH}+\widehat{BDH}=180^0\left(90^0+90^0=180^0\right)\)
Do đó: BEHD là tứ giác nội tiếp(Dấu hiệu nhận biết tứ giác nội tiếp)

a, E, F cùng nhìn BC dưới 1 góc 90 => tứ giác BFEC nội tiếp
cmtt F,E cung nhìn AH dưới 1 góc 90 => tứ giác AEHF nội tiếp =>góc EHC = góc BAC ( cùng bù với EHF)
b, Xét tam giác ABE và tam giác CHE có
góc BAC = góc EHC
góc BEA = góc CEH = 90
=>tam giác BAE đồng dạng với tam giác CHE(gg) =>AE/HE=BE/CE=> EA.EC=EH.EC
c,cmtt câu a, ta được tứ giác BFHD =>góc ABE = góc FDA
tứ giác DHEC nội tiếp =>góc ADE = góc FCA
Lại có góc ABE = góc FCA vì cùng phụ với góc BAC => góc FDA=góc ADE => AD là phân giác của góc FDE
cmtt =>FC và EB là phân giác của góc DFE và DEF
=> H là tâm đường tròn nội tiếp tam giác DEF

a) Xét tứ giác AEHF có
\(\widehat{HEA}+\widehat{HFA}=180^0\)
nên AEHF là tứ giác nội tiếp(Dấu hiệu nhận biết tứ giác nội tiếp)
Xét tứ giác AEDB có
\(\widehat{AEB}=\widehat{ADB}\left(=90^0\right)\)
nên AEHF là tứ giác nội tiếp(Dấu hiệu nhận biết tứ giác nội tiếp)

a: Xét tứ giác AEHF có
góc AEH+góc AFH=180 độ
=>AEHF là tứ giác nội tiếp
Xét tứ giác BFEC có
góc BFC=góc BEC=90 độ
=>BFEC là tứ giác nội tiếp
b: Xét (O) có
ΔABK nội tiếp
AK là đường kính
=>ΔABK vuông tại B
=>BK//CH
Xét (O) có
ΔACK nội tiếp
AK là đường kính
=>ΔACK vuông tại C
=>CK//BH
Xét tứ giác BHCK có
BH//CK
BK//CH
=>BHCK là hình bình hành
=>BC cắt HK tại trung điểm của mỗi đường
=>I là trung điểm của BC

a) Xét tứ giác AEHF có
\(\widehat{AFH}\) và \(\widehat{AEH}\) là hai góc đối
\(\widehat{AFH}+\widehat{AEH}=180^0\left(90^0+90^0=180^0\right)\)
Do đó: AEHF là tứ giác nội tiếp(Dấu hiệu nhận biết tứ giác nội tiếp)
b) Xét tứ giác BFEC có
\(\widehat{BFC}=\widehat{BEC}\left(=90^0\right)\)
\(\widehat{BFC}\) và \(\widehat{BEC}\) là hai góc cùng nhìn cạnh BC
Do đó: BFEC là tứ giác nội tiếp(Dấu hiệu nhận biết tứ giác nội tiếp)