
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(B=\left(x-1\right)\left(x+6\right)\left(x+2\right)\left(x+3\right)\)
\(=\left(x^2+5x-6\right)\left(x^2+5x+6\right)\)
\(=\left(x^2+5x\right)^2-36\ge-36\)
\(B_{min}=-36\) khi \(\left[{}\begin{matrix}x=0\\x=-5\end{matrix}\right.\)
\(C=\left(x^2-2x+1\right)+\left(y^2-4y+4\right)+2\)
\(=\left(x-1\right)^2+\left(y-2\right)^2+2\ge2\)
\(C_{min}=2\) khi \(\left(x;y\right)=\left(1;2\right)\)
b) Ta có: \(B=\left(x-1\right)\left(x+2\right)\left(x+3\right)\left(x+6\right)\)
\(=\left(x^2+5x-6\right)\left(x^2+5x+6\right)\)
\(=\left(x^2+5x\right)^2-36\ge-36\forall x\)
Dấu '=' xảy ra khi x(x+5)=0
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=-5\end{matrix}\right.\)
Vậy: \(B_{min}=-36\) khi \(x\in\left\{0;-5\right\}\)
c) Ta có: \(C=x^2-2x+y^2-4y+7\)
\(=x^2-2x+1+y^2-4y+4+2\)
\(=\left(x-1\right)^2+\left(y-2\right)^2+2\ge2\forall x,y\)
Dấu '=' xảy ra khi \(\left\{{}\begin{matrix}x=1\\y=2\end{matrix}\right.\)
Vậy: \(C_{min}=2\) khi (x,y)=(1;2)

Vì \(AB//CD\) nên \(\left\{{}\begin{matrix}\widehat{B}+\widehat{C}=180^0\\\widehat{A}+\widehat{D}=180^0\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}\widehat{B}=\left(180^0+40^0\right):2=110^0\\3\widehat{D}=180^0\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}\widehat{C}=180^0-110^0=70^0\\\widehat{D}=60^0\end{matrix}\right.\Rightarrow\widehat{A}=120^0\)
\(\widehat{B}=110^0\)
\(\widehat{C}=70^0\)
\(\widehat{A}=120^0\)
\(\widehat{D}=60^0\)

gọi x là sp mỗi đội làm theo kế hoạch (x>0)
=> số ngày là xong là 216/x (ngày)
theo đb => pt:
\(3x+\left(x+8\right)\left(\dfrac{216}{x}-3-1\right)=232\\ \Leftrightarrow3x+\left(x+8\right)\left(\dfrac{216-4x}{x}\right)=232\)
\(\Leftrightarrow3x^2+\left(x+8\right)\left(216-4x\right)=232x\\ \Leftrightarrow3x^2+184x-4x^2+1728-232x=0\\ \Leftrightarrow x^2+48x-1728=0\\ \Leftrightarrow\left(x-24\right)\left(x+72\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=24\left(tm\right)\\x=-72\left(l\right)\end{matrix}\right.\)
-Gọi số áo mỗi ngày tổ định dệt theo kế hoạch là x (áo) (x>0).
-Tổng số áo tổ dệt len phải dệt không tính 3 ngày đầu theo kế hoạch là: \(216-3x\left(áo\right)\)
Tổng số áo Số áo/ngày Số ngày dệt
(không tính 3 ngày đầu) (sau 3 ngày đầu) (không tính 3 ngày đầu)
Kế hoạch \(216-3x\) x \(\dfrac{216-3x}{x}\)
Thực tế \(232-3x\) x+8 \(\dfrac{232-3x}{x+8}\)
-Tổng số áo tổ dệt len phải dệt không tính 3 ngày đầu trên thực tế là: \(216-3x\left(áo\right)\)
-Số áo tổ dệt được trong 1 ngày sau 3 ngày đầu theo kế hoạch là: x (áo)
-Số áo tổ dệt được trong 1 ngày sau 3 ngày đầu trên thực tế là: x+8 (áo)
-Số ngày dệt không tính 3 ngày đầu theo kế hoạch là: \(\dfrac{216-3x}{x}\) (ngày)
-Số ngày dệt không tính 3 ngày đầu trên thực tế là: \(\dfrac{232-3x}{x+8}\) (ngày)
-Vì tổ hoàn thành kế hoạch trước thời hạn 1 ngày nên ta có phương trình:
\(\dfrac{216-3x}{x}-\dfrac{232-3x}{x+8}=1\)
\(\Leftrightarrow\dfrac{\left(216-3x\right)\left(x+8\right)}{x\left(x+8\right)}-\dfrac{\left(232-3x\right)x}{x\left(x+8\right)}=\dfrac{x\left(x+8\right)}{x\left(x+8\right)}\)
\(\Rightarrow216x+1728-3x^2-24x-232x+3x^2=x^2+8x\)
\(\Leftrightarrow1728-40x=x^2+8x\)
\(\Leftrightarrow x^2+48x-1728=0\)
\(\Leftrightarrow x^2-24x+72x-1728=0\)
\(\Leftrightarrow x\left(x-24\right)+72\left(x-24\right)=0\)
\(\Leftrightarrow\left(x-24\right)\left(x+72\right)=0\)
\(\Leftrightarrow x=24\left(nhận\right)\) hay \(x=-72\left(loại\right)\)
-Vậy số áo mỗi ngày tổ định dệt theo kế hoạch là 24 áo.

a: Ta có: AH\(\perp\)BD
CK\(\perp\)BD
Do đó: AH//CK
b: Xét ΔADH vuông tại H và ΔCBK vuông tại K có
AD=CB
\(\widehat{ADH}=\widehat{CBK}\)
Do đó: ΔADH=ΔCBK
Suy ra: AH=CK
Xét tứ giác AHCK có
AH//CK
AH=CK
Do đó: AHCK là hình bình hành
Suy ra: AK//CH

30: Ta có: \(5x-5y+ax-ay\)
\(=5\left(x-y\right)+a\left(x-y\right)\)
\(=\left(x-y\right)\left(a+5\right)\)
31: Ta có: \(6x^2-11x+3\)
\(=6x^2-9x-2x+3\)
\(=\left(2x-3\right)\left(3x-1\right)\)



\(6x^2+xy-7x-2y^2+7y-5=-\left(y-2x-1\right)\left(2y+3x-5\right)\)
\(6x^2+xy-7x-2y^2+7y-5=-2y\left(y-2x-1\right)-3x\left(y-2x-1\right)+5\left(y-2x-1\right)=-\left(y-2x-1\right)\left(2y+3x-5\right)\)

Bài 4:
a: Ta có: \(\widehat{OAB}=\widehat{ODC}\)
\(\widehat{OBA}=\widehat{OCD}\)
mà \(\widehat{ODC}=\widehat{OCD}\)
nên \(\widehat{OAB}=\widehat{OBA}\)
hay ΔOAB cân tại O
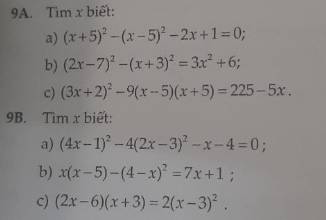
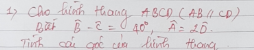


 Giúp mk lm bài này vs ạ
Giúp mk lm bài này vs ạ



Bài 9A:
\(a,\left(x+5\right)^2-\left(x-5\right)^2-2x+1=0\\ \Leftrightarrow\left(x^2+10x+25\right)-\left(x^2-10x+25\right)-2x+1=0\\ \Leftrightarrow x^2-x^2+10x+10x-2x=-1-25+25\\ \Leftrightarrow18x=-1\\ \Leftrightarrow x=-\dfrac{1}{18}\\ b,\left(2x-7\right)^2-\left(x+3\right)^2=3x^2+6\\ \Leftrightarrow4x^2-28x+49-x^2-6x-9-3x^2-6=0\\ \Leftrightarrow4x^2-x^2-3x^2-28x-6x=6+9-49\\ \Leftrightarrow22x=-34\\ \Leftrightarrow x=-\dfrac{17}{11}\\ c,\left(3x+2\right)^2-9\left(x-5\right)\left(x+5\right)=225-5x\\ \Leftrightarrow9x^2+12x+4-9\left(x^2-25\right)=225-5x\\ \Leftrightarrow9x^2-9x^2+12x+5x=225-4+9.25\\ \Leftrightarrow17x=446\\ \Leftrightarrow x=\dfrac{446}{17}\)
Sao bài này câu nào x cũng k nguyên ta, hơi xấu hi
9B
\(a,\left(4x-1\right)^2-4\left(2x-3\right)^2-x-4=0\\ \Leftrightarrow16x^2-8x+1-4\left(4x^2-12x+9\right)-x-4=0\\ \Leftrightarrow16x^2-16x^2-8x+48x-x=4+36-1\\ \Leftrightarrow39x=39\\ \Leftrightarrow x=1\\ b,x\left(x-5\right)-\left(4-x\right)^2=7x+1\\ \Leftrightarrow x^2-5x-\left(16-8x+x^2\right)-7x-1=0\\ \Leftrightarrow x^2-x^2-5x+8x-7x=1+16\\ \Leftrightarrow-4x=17\\ \Leftrightarrow x=\dfrac{-17}{4}\\ c,\left(2x-6\right)\left(x+3\right)=2\left(x-3\right)^2\\ \Leftrightarrow2x^2-6x+6x-18=2\left(x^2-6x+9\right)\\ \Leftrightarrow2x^2-2x^2-6x+6x+12x=18+18\\ \Leftrightarrow12x=36\\ \Leftrightarrow x=\dfrac{36}{12}=3\)