
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) Ta có: OA=OB(gt)
nên \(\dfrac{OA}{OB}=1\)(1)
Ta có: AC=BD(gt)
nên \(\dfrac{AC}{BD}=1\)(2)
Từ (1) và (2) suy ra \(\dfrac{OA}{OB}=\dfrac{AC}{BD}\)
hay \(\dfrac{OA}{AC}=\dfrac{OB}{BD}\)
Xét ΔOCD có
A∈OC(gt)
B∈OD(gt)
\(\dfrac{OA}{AC}=\dfrac{OB}{BD}\)(cmt)
Do đó: AB//CD(Định lí Ta lét đảo)
Ta có: OB+BD=OD(B nằm giữa O và D)
OA+AC=OC(A nằm giữa O và C)
mà OB=OA(gt)
và AC=BD(gt)
nên OD=OC
Xét ΔODC có OD=OC(cmt)
nên ΔODC cân tại O(Định nghĩa tam giác cân)
⇒\(\widehat{ODC}=\widehat{OCD}\)(hai góc ở đáy)
hay \(\widehat{ACD}=\widehat{BDC}\)
Xét tứ giác ABDC có AB//DC(cmt)
nên ABDC là hình thang có hai đáy là AB và DC(Định nghĩa hình thang)
Hình thang ABDC(AB//DC) có \(\widehat{ACD}=\widehat{BDC}\)(cmt)
nên ABDC là hình thang cân(Dấu hiệu nhận biết hình thang cân)


1)
a) 4y2-4xy+x2= x2-4xy+4y2= (x-2y)2
b) 9x2-12xy+4y2= (3x)2-2.3x.2y+(2y)2= (3x-2y)2
c) 16x2-25=(4x)2-52= (4x-5)(4x+5)
d) 1-9y2= 12-(3y)2=(1-3y)(1+3y)
g) x3-27y3= (x-3y)(x2+3xy+9y2)
h) 64 + 8x3=(4+2x)(16+8x+4x2)


b: \(N=a^3-3a^2-a\left(3-a\right)\)
\(=a^2\left(a-3\right)+a\left(a-3\right)\)
\(=a\left(a-3\right)\left(a+1\right)\)

Bài 5:
e: \(=\dfrac{x-5+2x+10-2x-10}{\left(x-5\right)\left(x+5\right)}=\dfrac{x-5}{\left(x-5\right)\left(x+5\right)}=\dfrac{1}{x+5}\)

4A:
a: \(A=3xy-2x+4x^2y^2\)
\(=3\cdot\left(-1\right)\cdot2-2\cdot\left(-1\right)+4\cdot\left(-1\right)^2\cdot2^2\)
\(=-6+2+16\)
=12

2:
a: =3x^2-3xy-(5x-5y)
=3x(x-y)-5(x-y)
=(x-y)(3x-5)
b: =6x(2x-y)-3y(2x-y)
=(2x-y)(6x-3y)
=3(2x-y)^2
c: =x(a-b)-y(a-b)
=(a-b)(x-y)
d: =x^2(a-b)-y^2(a-b)
=(a-b)(x^2-y^2)
=(x-y)(x+y)(a-b)
e: \(=6y\left(2x^2-3xy-5y^2\right)\)
=6y(2x^2-5xy+2xy-5y^2)
=6y[x(2x-5y)+y(2x-5y)]
=6y(2x-5y)(x+y)
f: =5x(x-y)-10(x-y)
=(x-y)(5x-10)
=5(x-2)(x-y)
g: =3x-4x+3y-4y
=-x+y
h: =7x(x-y)+(x-y)
=(x-y)(7x+1)
k: =(5x)^2-(3x+3y)^2
=(5x-3y-3x)(5x+3x+3y)
=(8x+3y)*(2x-3y)
 Bài dưới thôi :33
Bài dưới thôi :33



 bài 2 thôi ạ
bài 2 thôi ạ  làm bài 5 thôi nhé
làm bài 5 thôi nhé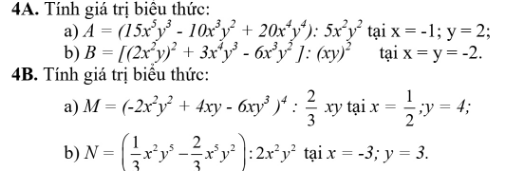
 chỉ làm bài 2 thôi
chỉ làm bài 2 thôi
Chọn B nhé bạn
chọn đáp án B