Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
M P N D E H K
a) Xét tam giác PMD và tam giác EMD, ta có :
PMD = EMD ( gt )
MD chung
MP = ME ( gt )
=> Tam giác PMD bằng Tam giác EMD ( c . g . c )
b) Xét tam giác MPK và tam giác MEK, ta có :
PMD = EMD ( gt )
MK chung
MP = ME ( gt )
=> Tam giác MPK = Tam giác MEK ( c . g .c )
=> KP = KE ( 1 )
=> MKE = MKP = 900 ( 2 )
Từ 1 và 2 suy ra MDlaf đường trung trực đoạn thẳng PE
c) Ta có MDN = MDH { ( 1800 - PDE ) + MDE }
Xét tam giác MHD và tam giác MND, ta có :
HMD = NMD ( gt )
MD chung
MDN = MDH ( gt )
=> Tam giác MHD bằng tam giác MND ( g . c .g )
=> HD = DN
d)
a)Xét \(\Delta ABI\)vuông tại A và \(\Delta KBI\)vuông tại K ,có:
\(\widehat{ABI}=\widehat{KBI}\)(do BI là phân giác của \(\widehat{ABC}\))
\(BI:chung\)
\(\Rightarrow\Delta ABI=\Delta KBI\left(ch.gn\right)\)
b)Vì \(\Delta ABI=\Delta KBI\left(ch.gn\right)\)
\(\Rightarrow\hept{\begin{cases}AB=KB\\AI=BI\end{cases}}\)(2 cạnh tương ứng)
\(\Rightarrow B,I\)thuộc đường trung trực của AK
hay BI là đường trung trực của AK
c)Vì BI là phân giác của \(\widehat{ABC}\)
\(\Rightarrow\)\(\widehat{ABI}=\widehat{KBI}=\frac{\widehat{ABC}}{2}=\frac{60^0}{2}=30^0=\widehat{ACB}\)(do \(\Delta ABC\)vuông tại A)
\(\Rightarrow\Delta BIC\)cân tại I
mà IK là đường cao
\(\Rightarrow IK\)là đường trung tuyến của \(\Delta BIC\)
\(\Rightarrowđpcm\)
//Sorry bạn nha .Hôm qua chỗ mình mưa to quá lại còn có sấm sét nữa nên mình không giải tiếp được cho bạn .
c)Vì \(\Delta BIC\)cân tại I nên IB=IC
Xét \(\Delta ABI\)vuông tại A ,có:
\(IB\)là cạnh huyền
\(\Rightarrow AB< IB=IC\)
d)Vì \(\Delta ABC\)vuông tại A \(\Rightarrow AB\perp AC\)
Xét \(\Delta BIC\),có:
BA,IK,CF là các đường cao
\(\Rightarrow BA,IK,CF\)đồng quy tại trực tâm của \(\Delta BIC\)
là số hữu tỉ âm.
là số hữu tỉ âm.
là số hữu tỉ dương.
là số hữu tỉ dương.
a) \(A=\frac{6n-1}{3n+1}=\frac{2\left(3n+1\right)-3}{3n+1}=2-\frac{3}{3n+1}\)
Để A đạt GTNN thì \(\frac{3}{3n-1}\) phải đạt giá trị lớn nhất
\(\Rightarrow\hept{\begin{cases}\frac{3}{3n-1}>0\\3n-1\text{ đạt giá trị nhỏ nhất}\end{cases}}\)
\(\Rightarrow\hept{\begin{cases}3n-1>0\\3n\text{ đạt giá trị nhỏ nhất}\end{cases}}\)
\(\Rightarrow\hept{\begin{cases}n>\frac{1}{3}\\n\text{ đạt giá trị nhỏ nhất}\end{cases}}\)
Mà n thuộc Z => n = 1
\(\Rightarrow A_{min}=\frac{6.1-1}{3.1+1}=\frac{5}{4}\Leftrightarrow n=1\)
b) Điều kiện để A là phân số:
\(\hept{\begin{cases}6n-1\inℤ\\3n+1\inℤ\\3n+1\ne0\end{cases}\Leftrightarrow\hept{\begin{cases}n\inℤ\\n\inℤ\\n\ne-\frac{1}{3}\end{cases}}}\)
Mà n thuộc Z => n luôn ≠ \(-\frac{1}{3}\)
Vậy để A là phân số thì n thuộc Z
c) A có giá trị nguyên <=> 6n - 1 chia hết cho 3n + 1
Có: 3n + 1 chia hết cho 3n + 1
=> 6n + 2 chia hết cho 3n + 1
=> 6n + 2 - (6n - 1) chia hết cho 3n + 1
=> 6n + 2 - 6n + 1 chia hết cho 3n + 1
=> 3 chia hết cho 3n + 1
=> 3n + 1 thuộc Ư(3) = {-3; -1; 1; 3}
=> 3n thuộc {-4; -2; 0; 2}
Mà n thuộc Z => 3n chia hết cho 3
=> 3n = 0
=> n = 0
Vậy để A thuộc Z thì n = 0
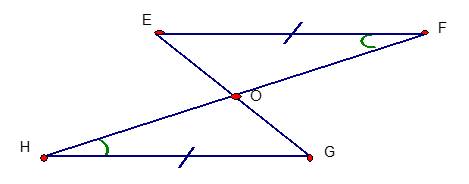
Xét \(\Delta EOFvà\Delta GOH\) có:
\(\widehat{H}=\widehat{F}\left(gt\right)\\ \widehat{EOF}=\widehat{GOH}\left(đđ\right)\\ GH=EF\)
=>\(\Delta EOF=\Delta GOH\left(c.g.c\right)\)
hg và ef sai cho mik xin lũi