Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài giải:
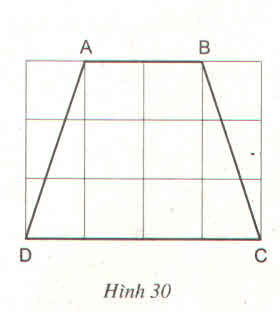
Theo hình vẽ, ta có: AB = 2cm, CD = 4cm
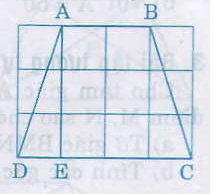
Trong tam giác vuông AED, áp dụng định lý Pitago ta được:
AD2 = AE2 + ED2
= 32 + 12 =10
Suy ra AD = √1010cm
Vậy AB = 2cm, CD = 4cm, AD = BC = √1010cm
A B C H D
Áp dụng định lí Pitago :
\(AD^2 = AH^2 + DH^2\)
\(= 3^2 + 1^2\)
\(= 10\)
\(\Rightarrow AD=\sqrt{10}\)
Vậy \(AB = 2cm\);\(CD = 4cm\);\(AD=BC=\sqrt{10}\)

Bài giải:
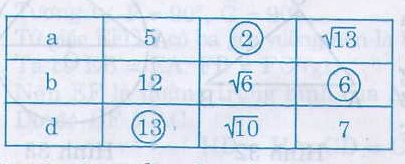
Cột thứ hai:
d2 = a2 + b2 = 52 + 122 = 25 + 144 = 169
Nên d = 13
Cột thứ ba:
a2 + b2 = d2 => a2 = d2 – b2=(√1010)2 - (√66)2
a2 = 10 – 6 = 4 => a = 2
Cột thứ tư:
a2 + b2 = d2 => b2 = d2 - a2 = 72 - (√1313)2
b2 = 49 – 13 = 36 => b = 6
Cột thứ hai:
d2 = a2 + b2 = 52 + 122 = 25 + 144 = 169
Nên d = 13
Cột thứ ba:
a2 + b2 = d2 => a2 = d2 – b2=(√1010)2 - (√66)2
a2 = 10 – 6 = 4 => a = 2
Cột thứ tư:
a2 + b2 = d2 => b2 = d2 - a2 = 72 - (√1313)2
b2 = 49 – 13 = 36 => b = 6

Lời giải
a)
Ta có \(\left\{{}\begin{matrix}MD=MB\\NA=NC\end{matrix}\right.\) \(\Rightarrow\)MN//DC
\(\Rightarrow\Delta OMN\approx\Delta ODC\approx OBA\)
Tỷ số đồng dạng
\(\dfrac{OM}{OD}=\dfrac{MN}{DC}=\dfrac{ON}{OC}\)\(\Rightarrow MN=\dfrac{OM}{OD}.DC=\dfrac{1}{4}.5,6=1,4\left(cm\right)\)
\(\dfrac{OM}{OB}=\dfrac{MN}{AB}\Rightarrow AB=\dfrac{OB}{OM}.MN=2MN=2,8\left(cm\right)\)
b)
\(\left\{{}\begin{matrix}CD=4MN\\AB=2MN\end{matrix}\right.\)
\(\Rightarrow\dfrac{CD-AB}{2}=\dfrac{4MN-2MN}{2}=MN\)

Ta có:
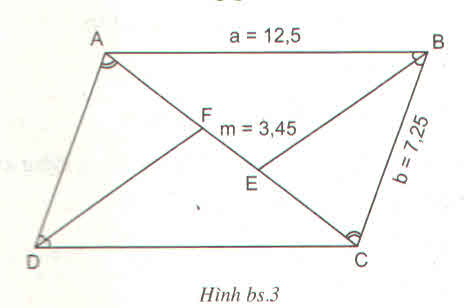
\(\widehat{ABC}=\widehat{ADC}\) và AD = BC = b = 7,25cm vì ABCD là hình bình hành.
Xét hai tam giác ADF và CBE ta có:
\(\widehat{ABC}=\widehat{ADC}\) (cmt)
AD = BC (cmt)
\(\widehat{DAF}=\widehat{BCE}\) (2 góc so le trong)
Vậy \(\Delta ADF=\Delta CBE\) (g-c-g).
=> AF = CE.
Cho AF = CE = x.
Áp dụng tính chất của đường phân giác BE trong tam giác ABC ta có:
\(\dfrac{AB}{BC}=\dfrac{AE}{CE}=\dfrac{AF+FE}{CE}\)
=> \(\dfrac{a}{b}=\dfrac{x+m}{x}=>x=\dfrac{mb}{a-b}\)= \(\dfrac{3,45.7,25}{12,5-7,25}=\dfrac{667}{140}\)
=> AC = \(2x+m=2.\dfrac{667}{140}+3,45=\dfrac{1817}{140}\approx12,98\)
Vậy AC \(\approx12,98\) cm.

Xin lỗi bn mink mới học có lớp 5 thôi à nên MINK ko thể giúp bn, xin lỗi nha




thank bn nhiều nhiều <:33