Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) cho A(x) = 0
\(=>2x^2-4x=0\)
\(x\left(2-4x\right)=0\Rightarrow\left[{}\begin{matrix}x=0\\4x=2\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=0\\x=\dfrac{1}{2}\end{matrix}\right.\)
b)\(B\left(y\right)=4y-8\)
cho B(y) = 0
\(4y-8=0\Rightarrow4y=8\Rightarrow y=2\)
c)\(C\left(t\right)=3t^2-6\)
cho C(t) = 0
\(=>3t^2-6=0=>3t^2=6=>t^2=2\left[{}\begin{matrix}t=\sqrt{2}\\t=-\sqrt{2}\end{matrix}\right.\)
d)\(M\left(x\right)=2x^2+1\)
cho M(x) = 0
\(2x^2+1=0\Rightarrow2x^2=-1\Rightarrow x^2=-\dfrac{1}{2}\left(vl\right)\)
vậy M(x) vô nghiệm
e) cho N(x) = 0
\(2x^2-8=0\)
\(2\left(x^2-4\right)=0\)
\(2\left(x^2+2x-2x-4\right)=0\)
\(2\left(x-2\right)\left(x+2\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x-2=0\\x+2=0\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=2\\x=-2\end{matrix}\right.\)

A: Đặt P(x)=0
=>3x-5=0
hay x=5/3
b: Đặt Q(x)=0
=>-2x+6=0
hay x=3
c: Đặt M(y)=0
=>1/2y-3=0
hay y=6
d: Đặt A(x)=0
=>12-3/4x=0
=>3/4x=12
hay x=16
Bài 7
a)cho P(x) = 0
\(=>3x-5=0\Leftrightarrow3x=5\Leftrightarrow x=\dfrac{5}{3}\)
b) cho Q(x) = 0
\(=>6-2x=0\Leftrightarrow2x=6\Leftrightarrow x=3\)
c)cho M(y) = 0
\(=>\dfrac{1}{2}y-3=0\Leftrightarrow\cdot\dfrac{1}{2}y=3\Leftrightarrow y=6\)
d)cho A(x) = 0
\(=>\dfrac{-3}{4}x+12=0=>-\dfrac{3}{4}x=-12=>x=16\)
e)cho B(y) = 0
=>\(2y+15=0=>2y=-15=>y=-\dfrac{15}{2}\)
f) cho C(t) = 0
=>\(2-5t=0=>5t=2=>t=\dfrac{2}{5}\)

a) `3x+5 =0`
`3x=-5`
`x=-5/3`
`b) -4x+8=0`
`-4x =-8`
`x=2`
`c) 3x -6=0`
`3x=6`
`x=2`
`d)x^2 +x =0`
`x(x+1) =0`
`=>[(x=0),(x=-1):}`
`e) x^2 -4 =0`
`x^2 =4`
`=> x = +-2`
`f) x^3 -27 =0`
`x^3 =27`
`=> x=3`
`g) 3x^2 +4 =0`
`3x^2 =-4`
`x^2 =-4/3(vô-lí)`
=> Đa thức ko có nghiệm
h) `x^3 -4x =0`
`x(x^2 -4) =0`
`=>[(x=0),(x^2=4 => x=+-2):}`
i) `2x^3 -32x =0`
`2x(x^2 -16)=0`
`=>[(2x=0),(x^2=16):}`
`=>[(x=0),(x=+-4):}`

a) Thay các giá trị – 1, 0, 1, 2 vào biểu thức ta được:
\(\begin{array}{l}3.( - 1) - 6 = - 3 - 6 = - 9\\3.0 - 6 = 0 - 6 = - 6\\3.1 - 6 = 3 - 6 = - 3\\3.2 - 6 = 6 - 6 = 0\end{array}\)
Vậy 2 là nghiệm của đa thức \(3x - 6\).
b) Thay các giá trị – 1, 0, 1, 2 vào biểu thức ta được:
\(\begin{array}{l}{( - 1)^4} - 1 = 1 - 1 = 0\\{0^4} - 1 = 0 - 1 = - 1\\{1^4} - 1 = 1 - 1 = 0\\{2^4} - 1 = 16 - 1 = 15\end{array}\)
Vậy 1 và – 1 là nghiệm của đa thức \({x^4} - 1\)
c) Thay các giá trị – 1, 0, 1, 2 vào biểu thức ta được:
\(\begin{array}{l}3.{( - 1)^2} - 4.( - 1) = 3 + 4 = 7\\{3.0^2} - 4.0 = 0 - 0 = 0\\{3.1^2} - 4.1 = 3 - 4 = - 1\\{3.2^2} - 4.2 = 12 - 8 = 4\end{array}\)
Vậy 0 là nghiệm của đa thức \(3{x^2} - 4x\).
d) Thay các giá trị – 1, 0, 1, 2 vào biểu thức ta được:
\(\begin{array}{l}{( - 1)^2} + 9 = 1 + 9 = 10\\{0^2} + 9 = 0 + 9 = 9\\{1^2} + 9 = 1 + 9 = 10\\{2^2} + 9 = 4 + 9 = 13\end{array}\)
Vậy không giá trị nào là nghiệm của đa thức \({x^2} + 9\).

a: C=A-B
\(=5x^3+y^3-3x^2y+4xy^2-4x^3+6x^2y-xy^2\)
\(=x^3+3x^2y+3xy^2+y^3\)
D=A+B
\(=5x^3+y^3-3x^2y+4xy^2+4x^3-6x^2y+xy^2\)
\(=9x^3-9x^2y+5xy^2+y^3\)
bậc của C là 3
bậc của D là 3
b: Thay x=0 và y=-2 vào D, ta được:
\(D=9\cdot0^3-9\cdot0^2\left(-2\right)+5\cdot0\cdot\left(-2\right)^2+\left(-2\right)^3\)
\(=0-0+0-8=-8\)
c: Thay x=-1 và y=-1 vào C, ta được:
\(C=\left(-1\right)^3+3\cdot\left(-1\right)^2\cdot\left(-1\right)+3\cdot\left(-1\right)\cdot\left(-1\right)^2+\left(-1\right)^3\)
=-8

b: 1/2x-4=0
=>1/2x=4
hay x=8
a: x+7=0
=>x=-7
e: 4x2-81=0
=>(2x-9)(2x+9)=0
=>x=9/2 hoặc x=-9/2
g: x2-9x=0
=>x(x-9)=0
=>x=0 hoặc x=9

a: x+7=0
nên x=-7
b: x-4=0
nên x=4
c: -8x+20=0
=>-8x=-20
hay x=5/2
d: x2-100=0
=>(x-10)(x+10)=0
=>x=10 hoặc x=-10
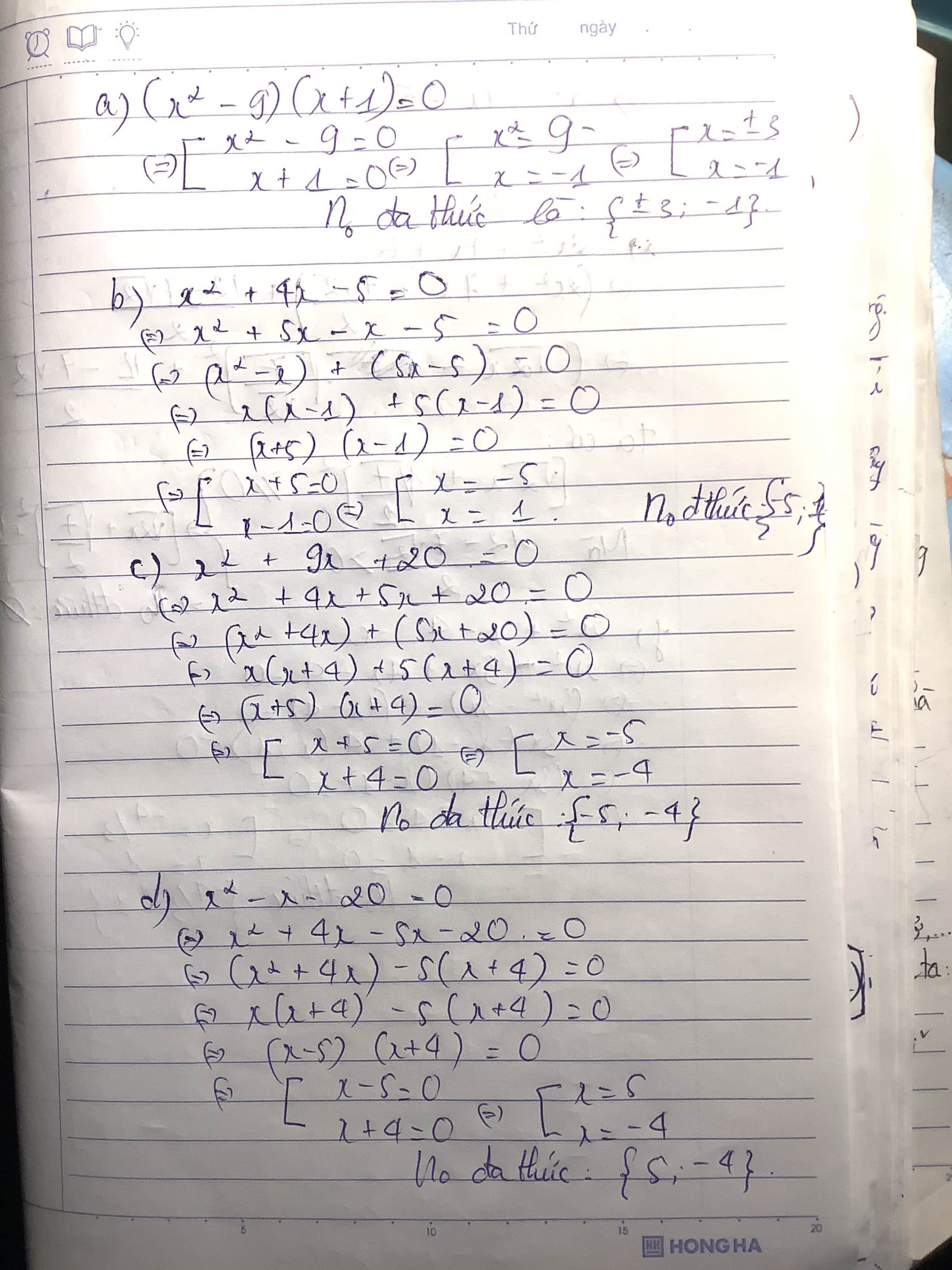

các bạn giúp mình zới nà
Bài 6 :
a) \(3x-5=0\)
\(3x=5\)
\(x=\frac{5}{3}\)
Vậy \(x=\frac{5}{3}\)là nghiệm A(x)
b) \(\left(x-3\right)\left(4x+7\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}x-3=0\\4x+7=0\end{cases}\Leftrightarrow\orbr{\begin{cases}x=3\\x=-\frac{7}{4}\end{cases}}}\)
Vậy :...
c) \(9x^2-16=0\)
\(\Leftrightarrow\left(3x-4\right)\left(3x+4\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}3x-4=0\\3x+4=0\end{cases}\Leftrightarrow\orbr{\begin{cases}x=\frac{4}{3}\\x=-\frac{4}{3}\end{cases}}}\)
d) \(x^3-4x=0\)
\(\Leftrightarrow x\left(x^2-4\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}x=0\\x^2-4=0\end{cases}\Leftrightarrow\orbr{\begin{cases}x=0\\x=\pm2\end{cases}}}\)
Bài 7 :
a) \(2y-7=0\)
\(\Leftrightarrow2y=7\)
\(\Leftrightarrow y=\frac{7}{2}\)
b) \(\left(y+5\right)\left(4y-9\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}y+5=0\\4y-9=0\end{cases}\Leftrightarrow\orbr{\begin{cases}x=-5\\y=\frac{9}{4}\end{cases}}}\)
c)\(y^2-25=0\)
\(\Leftrightarrow y^2=25\)
\(\Leftrightarrow y=\pm5\)
d) \(y^3+27=0\)
\(\Leftrightarrow y^3=-27\)
\(\Leftrightarrow y=-3\)
#H