Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

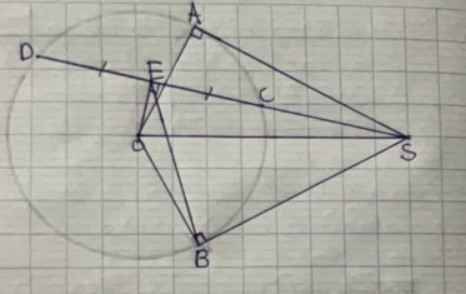
Xét tứ giác SOAB có: \(\left\{{}\begin{matrix}\widehat{SAO}=90^o\\\widehat{SBO}=90^o\end{matrix}\right.\)
=> Tứ giác SOAB nội tiếp (tổng 2 góc đối = 180o).
=> 4 điểm S, A, O, B cùng thuộc 1 đường tròn.

1: Xét tứ giác SAOB có
góc SAO+góc SBO=180 độ
=>SAOB là tứgiác nội tiếp
b: ΔOCD cân tại O
mà OE là trung tuyến
nên OE vuông góc CD
Xét tứ giác OESB có
góc OES+góc OBS=180 độ
=>OESB là tứ giác nội tiếp
=>góc SEB=góc SOB=1/2*góc AOB
=>góc AOB=2*góc SEB

1: góc OAS+góc OBS=90+90=180 độ
=>OASB nội tiép
2: Xét ΔSAC và ΔSDA có
góc SAC=góc SDA
góc ASC chung
=>ΔSAC đồng dạng với ΔSDA
=>SA/SD=SC/SA
=>SA^2=SD*SC=SA*SB
3: Xét (O) có
SA,SB là tiêp tuyến
=>SA=SB
mà OA=OB
nên OS là trung trực của AB
=>OS vuông góc AB tại I
=>SI*SO=SA^2=SC*SD
=>SI/SD=SC/SO
=>ΔSIC đồng dạng với ΔSDO

\(a.\Delta MAD\&\Delta MBA:\widehat{MAD}=\widehat{MBA}\left(=\frac{1}{2}\widebat{AD}\right);\widehat{AMB}=\widehat{AMD}\Rightarrow\Delta MAD~\Delta MBA\left(g.g\right)\Rightarrow MD^2=MB.MC\)b.Do I là trung điểm dây CD nên OI vuông góc CD mà ^SBO=90=>S;B;O;I cùng thuộc một đtròn
Mà dễ thấy S;B;A;O cùng thuộc một đtròn nên S;B;I;O;A cùng thuộc một đtròn
Do đó ^SIA=^SBA,^SIB=^SAB.Mà ^SAB=^SBA(do SA,SB là tiếp tuyến (O))=>^SIA=^SIB=>Đpcm
c.^DIE=^DCA=^DBE=>B;D;E;I cùng thuộc một đtròn=>^DEB=^DIB=^SAB=>DE//SA=>DE//BC
d.

a. Em tự giải
b.
Từ câu a ta có SAOB nội tiếp
Mà \(SA=SB\) (t/c hai tiếp tuyến cắt nhau)
\(\Rightarrow\widehat{SEA}=\widehat{SEB}\) (hai góc nt chắn 2 cùng bằng nhau của đường tròn ngoại tiếp SAOB)
\(\Rightarrow\widehat{AEB}=2\widehat{SEB}\) (1)
Do E là trung điểm CD \(\Rightarrow SE\perp CD\)
\(\Rightarrow E,A,B\) cùng nhìn SO dưới 1 góc vuông nên S,A,E,B,O cùng thuộc 1 đường tròn
Hay SAEB nội tiếp
\(\Rightarrow\widehat{AEB}+\widehat{ASB}=180^0\)
Theo câu a SAOB nội tiếp \(\Rightarrow\widehat{AOB}+\widehat{ASB}=180^0\)
\(\Rightarrow\widehat{AEB}=\widehat{AOB}\) (2)
(1);(2) \(\Rightarrow\widehat{AOB}=2\widehat{SEB}\)