
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


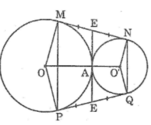
Kẻ tiếp tuyến chung tại A cắt MN tại E và PQ tại F
Trong đường tròn (O), theo tính chất hai tiếp tuyến cắt nhau, ta có:
EM = EA và FP = FA
Trong đường tròn (O’), theo tính chất hai tiếp tuyến cắt nhau, ta có:
EN = EA và FQ = FA
Suy ra: EM = EA = EN = (1/2).MN
FP = FA = FQ = (1/2).PQ
Suy ra : MN + PQ = 2EA + 2FA = 2(EA + FA) = 2EF (9)
Vì EF là đường trung bình của hình thang MNQP nên :
EF = (MP + NQ)/2 hay MP + NQ = 2EF (10)
Từ (9) và (10) suy ra: MN + PQ = MP + NQ

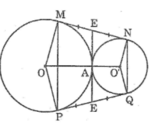
Ta có: MN ⊥ OM (tính chất tiếp tuyến)

Suy ra: QP ⊥ OP tại P
Vậy PQ là tiếp tuyến của đường tròn (O).
Ta có: MN ⊥ O’N (tính chất tiếp tuyến)

Suy ra: QP ⊥ O’Q tại Q

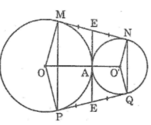
Vì M và P đối xứng qua trục OO’ nên OO’ là đường trung trực của MP
Suy ra: OP = OM
Khi đó P thuộc (O) và MP ⊥ OO’ (1)
Vì N và Q đối xứng qua trục OO’ nên OO’ là đường trung trực của NQ
Suy ra: O’N = O’Q
Khi đó Q thuộc (O’) và NQ ⊥ OO’ (2)
Từ (1) và (2) suy ra: MP // NQ
Tứ giác MNQP là hình thang
Vì OO’ là đường trung trực của MP và NQ nên OO’ đi qua trung điểm hai đáy hình thang MNQP, OO’ đồng thời cũng là trục đối xứng của hình thang MNQP nên MNQP là hình thang cân.
