Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

 c: Ta có: ΔOAB cân tại O
c: Ta có: ΔOAB cân tại O
mà OE là đường phân giác
nên OE\(\perp\)AB

cho góc nhọn xoy oz là tia phân giác của góc đó. Trên tia Ox lấy điểm A, trên tia Oy lấy điểm B sao cho OA = OB. Gọi I là giao điểm của Oz và AB
a) Chứng minh: Góc BIM = Góc AIN
b) Chứng minh: MN // AB
M,N ở đâu ra

a) Xét tam giác \(OIA\) và tam giác \(OIB\) có:
\(OA=OB\)
\(\widehat{AOI}=\widehat{BOI}\)
\(OI\) cạnh chung
suy ra \(\Delta OIA=\Delta OIB\) (c.g.c)
b) Xét tam giác \(OIN\) và tam giác \(OIM\):
\(\widehat{ION}=\widehat{IOM}\)
\(OI\) cạnh chung
\(\widehat{ONI}=\widehat{OMI}\left(=90^o\right)\)
suy ra \(\Delta OIN=\Delta OIM\) (cạnh huyền - góc nhọn)
\(\Rightarrow IN=IM\)
c) \(\Delta OIA=\Delta OIB\) suy ra \(IA=IB\).
Xét tam giác \(INA\) và tam giác \(IMB\):
\(IA=IB\)
\(\widehat{INA}=\widehat{IMB}\left(=90^o\right)\)
\(IN=IM\)
suy ra \(\Delta INA=\Delta IMB\) (cạnh huyền - cạnh góc vuông)
\(\Rightarrow\widehat{AIN}=\widehat{BIM}\)
d) \(\Delta OIN=\Delta OIM\) suy ra \(ON=OM\)
suy ra \(\dfrac{ON}{OA}=\dfrac{OM}{OB}\) suy ra \(MN//AB\).

a: Xét ΔOAB có OA=OB
nên ΔOAB cân tại O
mà OI là đường phân giác
nên I là trung điểmcủa AB
=>IA=IB
b: Xét tứ giác OBEA có
I là trung điểm của OE
I là trung điểm của BA
Do đó: OBEA là hình bình hành
Suy ra: BE//OA

a: Xét ΔAOM và ΔBOM có
OA=OB
góc AOM=góc BOM
OM chung
=>ΔAOM=ΔBOM
b: ΔOAB cân tại O
mà OI là phân giác
nen OI vuông góc AB
=>ΔMIA vuông tại I
c: Xét ΔMIA vuông tại I và ΔMIBvuông tại I có
MA=MB
MI chung
=>ΔMIA=ΔMIB

a.Xét $\triangle$OAI và $\triangle$OBI có:
$\widehat{AOI}$ = $\widehat{BOI}$(OI là phân giác của $\widehat{xOy}$)
OB = OA(gt)
OI chung
=> $\triangle$OAI = $\triangle$OBI(c-g-c)
=>$\widehat{OIA}$ = $\widehat{OIB}$(2 góc t/ứ)
mà $\widehat{OIA}$ + $\widehat{OIB}$ = $180^0$
=>$\widehat{OIA}$ = $\widehat{OIB}$ = $180^0$ : 2 = $90^0$
=> OI$\bot$AB(đpcm)
b.Xét $\triangle$OBA có
AD là đng cao t/ứ vs OB(gt)
OI là đng cao t/ứ vs AB(cmt)
AD cắt OI tại C(gt)
=>C là trực tâm của $\triangle$OBA(tính chất 3 đng cao của $\triangle$)
=>BC ⊥Ox(đpcm)

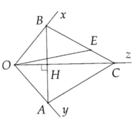
a: Xét tứ giác BOAE có
I là trung điểm của BA
I là trung điểm của OE
Do đó: BOAE là hình bình hành
Suy ra: BE//OA