Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Do ABCD là hình vuông
⇒ BC = CD = DA = AB = 4 (cm)
∠A = ∠B = ∠C = ∠D = 90⁰

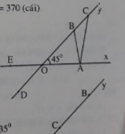
a) Có ba tam giác được tạo thành, đó là:
∆OAB,∆OAC,∆ABC.
b) Các góc kề bù với góc AOB là:
A O D ^ , B O E ^
A O B ^ và A O D ^ kề bù,
Nên A O B ^ + A O D ^ = 180 °
45 ° + A O D ^ = 180o; A O D ^ = 180 ° - 45 ° = 135 ° ;
Tương tự B O E ^ = 135 ° ;
c) Xảy ra hai trường hợp:
OC = 8 cm hoặc OC = 2 cm

Tiếp nhé
nên DB<DM (do 3cm,\(\frac{9}{2}\)cm). Suy ra điểm B nằm giữa 2 điểm D và M. Ta có:
DB+MB=DM
MB=\(\frac{9}{2}\)-3=4,5-3=1.5 (cm)
c, Theo ý a ta có điểm B nằm giữa D và C. Suy ra tia AB nằm giữa 2 tia AD và AC (1)
Ta có: \(\widehat{DAB}\) + \(\widehat{BAC}\) = \(\widehat{DAC}\) (*)
Vì tia Ay là tpg của DAB suy ra:
+Tia Ay nằm giữa 2 tia AD và AB (2)
+\(\widehat{DAy}\) = \(\widehat{yAB}\) = \(\frac{1}{2}\)\(\widehat{DAB}\)= \(\widehat{\frac{DAB}{2}}\) (**)
Vì tia Ax là tpg của BAC suy ra:
+Tia Ax nằm giữa 2 tia BA và BC (3)
+\(\widehat{BAx}\) = \(\widehat{xAC}\) = \(\frac{\widehat{BAC}}{2}\) (***)
Từ (1) (2) và (3) suy ra tia AB nằm giữa 2 tia Ax và Ay. Ta có:
\(\widehat{yAx}\) = \(\widehat{yAB}\) + \(\widehat{BAx}\) = \(\frac{\widehat{DAB}}{2}\)+ \(\frac{\widehat{BAC}}{2}\)
= \(\frac{D\widehat{AB}+\widehat{BAC}}{2}\) = \(\frac{\widehat{DAC}}{2}\)= 120o : 2 = 60o
a) Hình vuông có bốn cạnh bằng nhau nên ��=��=��=��=4AB=BC=CD=DA= 4 cm
Vì bốn góc đỉnh �A, �B, �C, �D bằng nhau nên số đo của các đỉnh là = 90∘90 độ
trả lời
Hình vuông có bốn cạnh bằng nhau nên ��=��=��=��=4AB=BC=CD=DA= 4 cm
Vì bốn góc đỉnh �A, �B, �C, �D bằng nhau nên số đo của các đỉnh là = 90∘90 độ