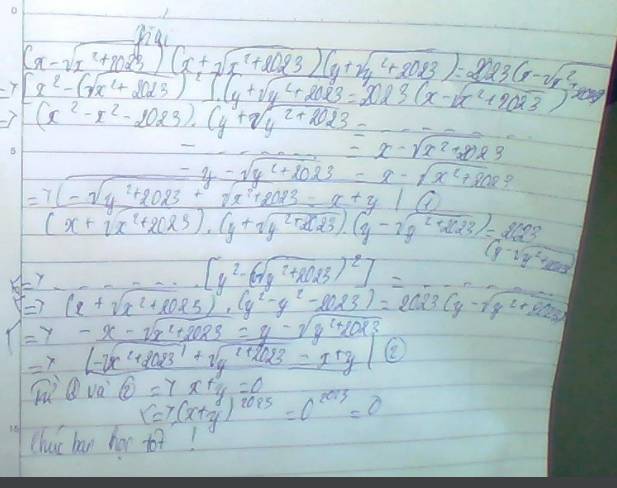TD
0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NV
1
NV
1
LD
7 tháng 4 2023
\(\sqrt{2023-\sqrt{x}}=2023-x\left(ĐK:x\ge0\right)\)
Đặt \(t=\sqrt{x}\left(t\le2023\right)\)
Pt trở thành : \(\sqrt{2023-t}=2023-t^2\)
\(\Leftrightarrow2023-t=\left(2023-t^2\right)^2\)
\(\Leftrightarrow t^4-4046t+4092529=2023-t\)
\(\Leftrightarrow t^4-4045+4090506=0\)
\(\Leftrightarrow\left[{}\begin{matrix}t=2023\left(n\right)\\t=2022\left(n\right)\end{matrix}\right.\)
+) Với \(t=2023\Rightarrow x^2=2023\Rightarrow x=\pm17\sqrt{7}\)
+) Với \(t=2022\Rightarrow x^2=2022\Leftrightarrow x=\pm\sqrt{2022}\)
Vì \(x\ge0\) \(\Rightarrow x\in\left\{17\sqrt{7};\sqrt{2022}\right\}\)
Vậy \(S=\left\{17\sqrt{7};\sqrt{2022}\right\}\)
29 tháng 10 2023
ĐKXĐ: x+7>=0
=>x>=-7
\(x^2+\sqrt{x+7}=7\)
=>\(x^2-4-3+\sqrt{x+7}=0\)
=>\(\left(x-2\right)\left(x+2\right)+\sqrt{x+7}-3=0\)
=>\(\left(x-2\right)\left(x+2\right)+\dfrac{x+7-9}{\sqrt{x+7}+3}=0\)
=>\(\left(x-2\right)\left(x+2+\dfrac{1}{\sqrt{x+7}+3}\right)=0\)
=>x-2=0
=>x=2(nhận)
AH
Akai Haruma
Giáo viên
29 tháng 4 2023
Bài 1: ĐKXĐ: $2\leq x\leq 4$
PT $\Leftrightarrow (\sqrt{x-2}+\sqrt{4-x})^2=2$
$\Leftrightarrow 2+2\sqrt{(x-2)(4-x)}=2$
$\Leftrightarrow (x-2)(4-x)=0$
$\Leftrightarrow x-2=0$ hoặc $4-x=0$
$\Leftrightarrow x=2$ hoặc $x=4$ (tm)
AH
Akai Haruma
Giáo viên
29 tháng 4 2023
Bài 2:
PT $\Leftrightarrow 4x^3(x-1)-3x^2(x-1)+6x(x-1)-4(x-1)=0$
$\Leftrightarrow (x-1)(4x^3-3x^2+6x-4)=0$
$\Leftrightarrow x=1$ hoặc $4x^3-3x^2+6x-4=0$
Với $4x^3-3x^2+6x-4=0(*)$
Đặt $x=t+\frac{1}{4}$ thì pt $(*)$ trở thành:
$4t^3+\frac{21}{4}t-\frac{21}{8}=0$
Đặt $t=m-\frac{7}{16m}$ thì pt trở thành:
$4m^3-\frac{343}{1024m^3}-\frac{21}{8}=0$
$\Leftrightarrow 4096m^6-2688m^3-343=0$
Coi đây là pt bậc 2 ẩn $m^3$ và giải ta thu được \(m=\frac{\sqrt[3]{49}}{4}\) hoặc \(m=\frac{-\sqrt[3]{7}}{4}\)
Khi đó ta thu được \(x=\frac{1}{4}(1-\sqrt[3]{7}+\sqrt[3]{49})\)
M
23 tháng 8 2023
Để tính (x+y)2023, ta sẽ sử dụng công thức nhân đa thức. Trước tiên, ta mở đuôi công thức:(x+y)2023 = (x+y)(x+y)(x+y)...(x+y)Từ phép nhân đầu tiên, ta có:(x+y)(x+y) = x^2 + 2xy + y^2Tiếp tục nhân với (x+y), ta có:(x^2 + 2xy + y^2)(x+y) = x^3 + 3x^2y + 3xy^2 + y^3Lặp lại quá trình này 2020 lần nữa, ta có:(x^3 + 3x^2y + 3xy^2 + y^3)(x+y) = x^4 + 4x^3y + 6x^2y^2 + 4xy^3 + y^4Tiếp tục nhân với (x+y), ta có:(x^4 + 4x^3y + 6x^2y^2 + 4xy^3 + y^4)(x+y) = x^5 + 5x^4y + 10x^3
AD
Cho \(\left(x+\sqrt{x^2+2023}\right)\left(y+\sqrt{y^2+2023}\right)=2023\)
Tính (x+y)2023
Help me plsss
0