TC
2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
15 tháng 9 2021
\(1,\sqrt{x+2+4\sqrt{x-2}}=5\left(x\ge2\right)\\ \Leftrightarrow\sqrt{\left(\sqrt{x-2}+4\right)^2}=5\\ \Leftrightarrow\sqrt{x-2}+4=5\\ \Leftrightarrow\sqrt{x-2}=1\\ \Leftrightarrow x-2=1\Leftrightarrow x=3\\ 2,\sqrt{x+3+4\sqrt{x-1}}=2\left(x\ge1\right)\\ \Leftrightarrow\sqrt{\left(\sqrt{x-1}+4\right)^2}=2\\ \Leftrightarrow\sqrt{x-1}+4=2\\ \Leftrightarrow\sqrt{x-1}=-2\\ \Leftrightarrow x\in\varnothing\left(\sqrt{x-1}\ge0\right)\)
\(3,\sqrt{x+\sqrt{2x-1}}=\sqrt{2}\left(x\ge\dfrac{1}{2};x\ne1\right)\\ \Leftrightarrow x+\sqrt{2x-1}=2\\ \Leftrightarrow x-2=-\sqrt{2x-1}\\ \Leftrightarrow x^2-4x+4=2x-1\\ \Leftrightarrow x^2-6x+5=0\\ \Leftrightarrow\left(x-5\right)\left(x-1\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=5\left(tm\right)\\x=1\left(loại\right)\end{matrix}\right.\)
\(4,\sqrt{x-2+\sqrt{2x-5}}=3\sqrt{2}\left(x\ge\dfrac{5}{2}\right)\\ \Leftrightarrow\sqrt{2x-4+2\sqrt{2x-5}}=6\\ \Leftrightarrow\sqrt{\left(\sqrt{2x-5}+1\right)^2}=6\\ \Leftrightarrow\sqrt{2x-5}+1=6\\ \Leftrightarrow\sqrt{2x-5}=5\\ \Leftrightarrow2x-5=25\Leftrightarrow x=15\left(TM\right)\)
17 tháng 5 2021
b, \(đk:x\ge2\)
Xét x=2 thay vào pt thấy không thỏa mãn => x>2 hay 27x-54>0
\(x^3-11x+36x-18=4\sqrt[4]{27x-54}\)
\(\Leftrightarrow27x^3-297x^2+972x-486=4\sqrt[4]{\left(27x-54\right).81.81.81}\le189+27x\) (cosi với 4 số dương, dấu = xảy ra khi x=5)
\(\Leftrightarrow x^3-11x^2+35x-25\le0\)
\(\Leftrightarrow\left(x-1\right)\left(x-5\right)^2\le0\) (*)
Có \(\left\{{}\begin{matrix}x>2\\\left(x-5\right)^2\ge0\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x-1>0\\\left(x-5\right)^2\ge0\end{matrix}\right.\)\(\Rightarrow\left(x-1\right)\left(x-5\right)^2\ge0\) (2*)
Từ (*) và (2*) ,dấu = xra khi x=5 (thỏa mãn)
Vây pt có nghiệm duy nhất x=5
17 tháng 5 2021
c,Có \(6\sqrt[3]{4x^3+x}=16x^4+5>0\)
\(\Leftrightarrow4x^3+x>0\)
Có: \(16x^4+5=6\sqrt[3]{4x^3+x}\le2\left(4x^3+x+2\right)\) (theo cosi với 3 số dương,dấu = xảy ra khi \(x=\dfrac{1}{2}\))
\(\Leftrightarrow16x^4-8x^3-2x+1\le0\)
\(\Leftrightarrow\left(2x-1\right)^2\left(4x^2+2x+1\right)\le0\) (*)
(tương tự câu b) Dấu = xảy ra khi \(x=\dfrac{1}{2}\)(thỏa mãn)
Vậy....
d) Đk: \(x\ge\dfrac{3}{4}\)
Áp dụng bđt cosi:
\(\sqrt{2x-1}\le\dfrac{2x-1+1}{2}=x\)
\(\Rightarrow\dfrac{1}{\sqrt{2x-1}}\ge\dfrac{1}{x}\) (*)
\(\sqrt[4]{4x-3}\le\dfrac{4x-3+1+1+1}{4}=x\)
\(\dfrac{\Rightarrow1}{\sqrt[4]{4x-3}}\ge\dfrac{1}{x}\) (2*)
Từ (*) và (2*) \(\Rightarrow\dfrac{1}{\sqrt{2x-1}}+\dfrac{1}{\sqrt[4]{4x-3}}\ge\dfrac{2}{x}\)
Dấu = xảy ra khi x=1 (tm)
23 tháng 10 2021
\(1,PT\Leftrightarrow2x-1=5\Leftrightarrow x=3\\ 2,\Leftrightarrow x-5=9\Leftrightarrow x=14\\ 3,ĐK:x\ge1\\ PT\Leftrightarrow3\sqrt{x-1}=21\Leftrightarrow\sqrt{x-1}=7\Leftrightarrow x=50\left(tm\right)\\ 4,\Leftrightarrow x=\dfrac{\sqrt{50}}{\sqrt{2}}=\dfrac{5\sqrt{2}}{\sqrt{2}}=5\)
TG
16 tháng 9 2021
a) \(3x-2\sqrt{x-1}=4\) (ĐK: x ≥ 1)
\(\Rightarrow3x-2\sqrt{x-1}-4=0\)
\(\Rightarrow3x-6-2\sqrt{x-1}+2=0\)
\(\Rightarrow3\left(x-2\right)-2\left(\sqrt{x-1}-1\right)=0\)
\(\Rightarrow3\left(x-2\right)-2.\dfrac{x-2}{\sqrt{x-1}+1}=0\)
\(\Rightarrow\left(x-2\right)\left[3-\dfrac{2}{\sqrt{x-1}+1}\right]=0\)
*TH1: x = 2 (t/m)
*TH2: \(3-\dfrac{2}{\sqrt{x-1}+1}=0\)
\(\Rightarrow3=\dfrac{2}{\sqrt{x-1}+1}\)
\(\Rightarrow3\sqrt{x-1}+3=2\)
\(\Rightarrow3\sqrt{x-1}=-1\) (vô lí)
Vậy S = {2}
b) \(\sqrt{4x+1}-\sqrt{x+2}=\sqrt{3-x}\) (ĐK: \(-\dfrac{1}{4}\le x\le3\) )
\(\Rightarrow\sqrt{4x+1}-3-\sqrt{x+2}+2-\sqrt{3-x}+1=0\)
\(\Rightarrow\dfrac{4x-8}{\sqrt{4x+1}+3}-\dfrac{x-2}{\sqrt{x+2}+2}+\dfrac{x-2}{\sqrt{3-x}+1}=0\)
\(\Rightarrow\left(x-2\right)\left(\dfrac{4}{\sqrt{4x+1}+3}-\dfrac{1}{\sqrt{x+2}+2}+\dfrac{1}{\sqrt{3-x}+1}\right)=0\)
=> x = 2
16 tháng 9 2021
\(a,3x-2\sqrt{x-1}=4\left(x\ge1\right)\\ \Leftrightarrow-2\sqrt{x-1}=4-3x\\ \Leftrightarrow4\left(x-1\right)=16-24x+9x^2\\ \Leftrightarrow9x^2-28x+20=0\\ \Leftrightarrow\left(x-2\right)\left(9x-10\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=2\left(tm\right)\\x=\dfrac{10}{9}\left(tm\right)\end{matrix}\right.\)
\(b,\sqrt{4x+1}-\sqrt{x+2}=\sqrt{3-x}\left(-\dfrac{1}{4}\le x\le3\right)\\ \Leftrightarrow4x+1+x+2-2\sqrt{\left(4x+1\right)\left(x+2\right)}=3-x\\ \Leftrightarrow-2\sqrt{\left(4x+1\right)\left(x+2\right)}=2-6x\\ \Leftrightarrow\sqrt{4x^2+9x+2}=3x-1\\ \Leftrightarrow4x^2+9x+2=9x^2-6x+1\\ \Leftrightarrow5x^2-15x-1=0\\ \Leftrightarrow\Delta=225+20=245\\ \Leftrightarrow\left[{}\begin{matrix}x=\dfrac{15-\sqrt{245}}{10}=\dfrac{15-7\sqrt{5}}{10}\left(ktm\right)\\x=\dfrac{15+\sqrt{245}}{10}=\dfrac{15+7\sqrt{5}}{10}\left(tm\right)\end{matrix}\right.\Leftrightarrow x=\dfrac{15+7\sqrt{5}}{10}\)
NV
Nguyễn Việt Lâm
Giáo viên
28 tháng 2 2021
Do \(x^6-x^3+x^2-x+1=\left(x^3-\dfrac{1}{2}\right)^2+\left(x-\dfrac{1}{2}\right)^2+\dfrac{1}{2}>0\) ; \(\forall x\) nên BPT tương đương:
\(\sqrt{13}-\sqrt{2x^2-2x+5}-\sqrt{2x^2-4x+4}\ge0\)
\(\Leftrightarrow\sqrt{4x^2-4x+10}+\sqrt{4x^2-8x+8}\le\sqrt{26}\) (1)
Ta có:
\(VT=\sqrt{\left(2x-1\right)^2+3^2}+\sqrt{\left(2-2x\right)^2+2^2}\ge\sqrt{\left(2x-1+2-2x\right)^2+\left(3+2\right)^2}=\sqrt{26}\) (2)
\(\Rightarrow\left(1\right);\left(2\right)\Rightarrow\sqrt{4x^2-4x+10}+\sqrt{4x^2-8x+8}=\sqrt{26}\)
Dấu "=" xảy ra khi và chỉ khi \(2\left(2x-1\right)=3\left(2-2x\right)\Leftrightarrow x=\dfrac{4}{5}\)
Vậy BPT có nghiệm duy nhất \(x=\dfrac{4}{5}\)
LT
15 tháng 3 2021
Bài 1:
a) \(A=\sqrt{8}+\sqrt{18}-\sqrt{32}\)
\(=2\sqrt{2}+3\sqrt{2}-4\sqrt{2}\)
\(=\sqrt{2}\)
b) \(B=\sqrt{9-4\sqrt{5}}-\sqrt{5}\)
\(=\sqrt{4-4\sqrt{5}+5}-\sqrt{5}\)
\(=\sqrt{\left(2-\sqrt{5}\right)^2}-\sqrt{5}\)
\(=\left|2-\sqrt{5}\right|-\sqrt{5}\)
\(=\sqrt{5}-2-\sqrt{5}\)
\(=-2\)
LT
15 tháng 3 2021
Bài 2:
a) \(\left\{{}\begin{matrix}2x-3y=4\\x+3y=2\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}3x=6\\x+3y=2\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x=2\\2+3y=2\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x=2\\y=0\end{matrix}\right.\)
Vậy phương trình có nghiệm là: \(\left\{{}\begin{matrix}x=2\\y=0\end{matrix}\right.\)
b) ĐKXĐ: \(x\ne\pm2\)
Với \(x\ne\pm2\), ta có:
\(\dfrac{10}{x^2-4}+\dfrac{1}{2-x}=1\)
\(\Leftrightarrow\dfrac{10}{\left(x-2\right)\left(x+2\right)}-\dfrac{1}{x-2}=1\)
\(\Leftrightarrow\dfrac{10-x-2}{x^2-4}=1\)
\(\Leftrightarrow\dfrac{8-x}{x^2-4}=1\)
\(\Rightarrow x^2-4=8-x\)
\(\Leftrightarrow x^2+x-12=0\)
\(\Leftrightarrow x^2-3x+4x-12=0\)
\(\Leftrightarrow x\left(x-3\right)+4\left(x-3\right)=0\)
\(\Leftrightarrow\left(x-3\right)\left(x+4\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x-3=0\\x+4=0\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}x=3\\x=-4\end{matrix}\right.\) (TM)
Vậy phương trình có tập nghiệm là: S ={3; -4}
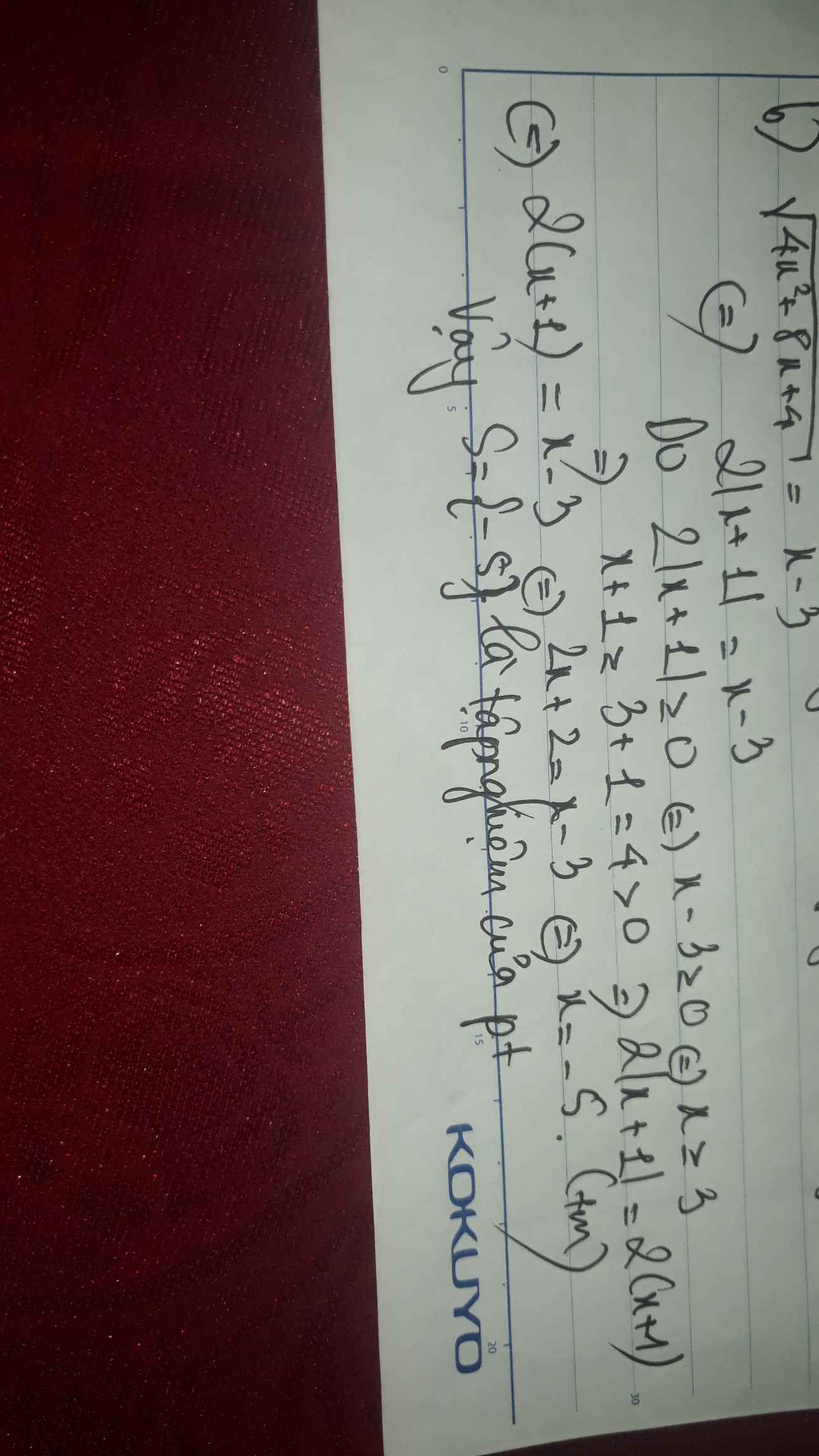
Sqrt5/2-x=4 với x bé hơn hoặc bằng 5/2