Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Ta có : \(x-1\inƯ\left(12\right)=\left\{\pm1;\pm2;\pm3;\pm4;\pm6;\pm12\right\}\)
...
b) Ta có : \(2x+1\inƯ\left(28\right)=\left\{\pm1;\pm2;\pm4;\pm7;\pm12;\pm28\right\}\)
Mà \(2x+1\)là số chẵn
\(\Rightarrow2x+1\in\left\{\pm1;\pm7\right\}\)
...
c) Ta có : \(x+15\)là bội của \(x+3\)
\(\Rightarrow x+15⋮x+3\)
\(\Rightarrow x+3+12⋮x+3\)
Vì \(x+3⋮x+3\)
\(\Rightarrow12⋮x+3\)
\(\Rightarrow x+3\inƯ\left(12\right)=\left\{\pm1;\pm2;\pm3;\pm4;\pm6;\pm12\right\}\)
...

\(a,12⋮x-1\)
\(x-1\inƯ\left(12\right)=\left\{\pm1;\pm2;\pm3;\pm4;\pm12\right\}\)
Ta lập bảng xét giá trị
x - 1 1 -1 2 -2 3 -3 4 -4 12 -12
x 2 0 3 -1 4 -2 5 -3 13 -11
\(c,x+15⋮x+3\)
\(x+3+12⋮x+3\)
\(12⋮x+3\)
Tự lập bảng , lười ~~~
\(d,\left(x+1\right)\left(y-1\right)=3\)
Ta lập bảng
| x+1 | 1 | -1 | 3 | -3 |
| y-1 | 3 | -3 | 1 | -1 |
| x | 2 | 0 | 2 | -4 |
| y | 4 | -2 | 2 | 0 |
i, Theo bài ra ta có : ( olm thiếu dấu và == nên trình bày kiủ nài )
\(x⋮10,x⋮12,x⋮15\)và \(100< x< 150\)
Gợi ý : Phân tích thừa số nguyên tố r xét ''BC'' ( chắc là BC )
:>> Hc tốt

\(a,12⋮x-1\)
\(x-1\inƯ\left(12\right)=\left\{\pm1;\pm2;\pm3;\pm4;\pm6;\pm12\right\}\)
Tự lập bảng nha
\(b,28⋮2x+1\)
\(2x+1\inƯ\left(28\right)=\left\{\pm1;\pm2;\pm7;\pm14\right\}\)
Ta có bảng
| 2x+1 | 1 | -1 | 2 | -2 | 7 | -7 | 14 | -14 |
| 2x | 0 | -2 | 1 | -3 | 6 | -8 | 13 | -15 |
| x | 0 | -1 | 1/2 | -3/2 | 3 | -4 | 13/2 | -15/2 |
\(c,x+15⋮x+3\)
\(x+3+12⋮x+3\)
\(12⋮x+3\)
\(\Rightarrow x+3\inƯ\left(12\right)=\left\{\pm1;\pm2;\pm3;\pm4;\pm6;\pm12\right\}\)
Tự lập bảng
\(d,\left(x+1\right)\left(y-1\right)=3\)
\(\Rightarrow x+1;y-1\inƯ\left(3\right)=\left\{\pm1;\pm3\right\}\)
Ta lập bảng
| x+1 | 1 | -1 | 3 | -3 |
| y-1 | 3 | -3 | 1 | -1 |
| x | 0 | -2 | 2 | -4 |
| y | 4 | -2 | 2 | 0 |

Bài 10:
a: 2x-3 là bội của x+1
=>\(2x-3⋮x+1\)
=>\(2x+2-5⋮x+1\)
=>\(-5⋮x+1\)
=>\(x+1\in\left\{1;-1;5;-5\right\}\)
=>\(x\in\left\{0;-2;4;-6\right\}\)
b: x-2 là ước của 3x-2
=>\(3x-2⋮x-2\)
=>\(3x-6+4⋮x-2\)
=>\(4⋮x-2\)
=>\(x-2\inƯ\left(4\right)\)
=>\(x-2\in\left\{1;-1;2;-2;4;-4\right\}\)
=>\(x\in\left\{3;1;4;0;6;-2\right\}\)
Bài 14:
a: \(4n-5⋮2n-1\)
=>\(4n-2-3⋮2n-1\)
=>\(-3⋮2n-1\)
=>\(2n-1\inƯ\left(-3\right)\)
=>\(2n-1\in\left\{1;-1;3;-3\right\}\)
=>\(2n\in\left\{2;0;4;-2\right\}\)
=>\(n\in\left\{1;0;2;-1\right\}\)
mà n>=0
nên \(n\in\left\{1;0;2\right\}\)
b: \(n^2+3n+1⋮n+1\)
=>\(n^2+n+2n+2-1⋮n+1\)
=>\(n\left(n+1\right)+2\left(n+1\right)-1⋮n+1\)
=>\(-1⋮n+1\)
=>\(n+1\in\left\{1;-1\right\}\)
=>\(n\in\left\{0;-2\right\}\)
mà n là số tự nhiên
nên n=0

2x-1 là ước của 12
=>\(2x-1\in\left\{1;-1;2;-2;3;-3;4;-4;6;-6;12;-12\right\}\)
mà 2x-1 không chia hết cho 2(do x là số tự nhiên)
nên \(2x-1\in\left\{1;-1;3;-3\right\}\)
=>\(2x\in\left\{2;0;4;-2\right\}\)
=>\(x\in\left\{1;0;2;-1\right\}\)
mà x là số tự nhiên
nên \(x\in\left\{0;1;2\right\}\)
x+13 chia hết cho x-1
=>\(x-1+14⋮x-1\)
=>\(14⋮x-1\)
=>\(x-1\in\left\{1;-1;2;-2;7;-7;14;-14\right\}\)
=>\(x\in\left\{2;0;3;-1;8;-6;15;-13\right\}\)
mà x là số tự nhiên
nên \(x\in\left\{2;0;3;8;15\right\}\)
4x+9 là bội của 2x+1
=>\(4x+9⋮2x+1\)
=>\(4x+2+7⋮2x+1\)
=>\(2x+1\in\left\{1;-1;7;-7\right\}\)
=>\(2x\in\left\{0;-2;6;-8\right\}\)
=>\(x\in\left\{0;-1;3;-4\right\}\)
mà x là số tự nhiên
nên \(x\in\left\{0;3\right\}\)

a)\(x-1\inƯ\left(24\right)=\left\{1;-1;2;-2;3;-3;4;-4;6;-6;8;-8;12;-12;24;-24\right\}\)
Vì \(x\in N\Rightarrow x-1\ge-1\)
\(\Rightarrow x-1\in\left\{1;-1;2;3;4;6;8;12;24\right\}\)
\(\Rightarrow x\in\left\{2;0;3;4;5;7;9;13;25\right\}\)
b) 36 là bội của \(2x-1\)
\(\Rightarrow2x-1\inƯ\left(36\right)\)
Mà \(2x+1⋮̸2\)
\(\Rightarrow2x+1\in\left\{1;-1;3;-3;9;-9\right\}\)
\(\Rightarrow2x\in\left\{0;-2;2;-4;8;-10\right\}\)
\(\Rightarrow x\in\left\{0;-1;1;-2;4;-10\right\}\)
Mà \(x\in N\)\(\Rightarrow x\in\left\{0;1;4\right\}\)
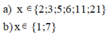
Bài 3:
x-1 thuoc Ư(4)={1;2;4}
TH1: x-1=1 TH2: x-1=2
x=2 x=3
TH3: x-1=4
x=5
=>x thuộc {2;3;5}