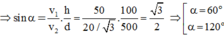Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài này nên dùng đạo hàm :3
Thời gian để ng đó bơi thẳng đến B là
\(t=\frac{d}{v_2}\left(h\right)\)
Thời gian để ng đó chay 1 quãng là a-x r bơi đến B là (x là khoảng cách từ nơi mà ng chạy đến rồi nhảy đến hình chiếu của B hạ xuống mp)
\(t=\frac{a-x}{v_1}+\frac{\sqrt{x^2+d^2}}{v_2}\)
\(t'=\frac{-1}{v_1}+\frac{1}{v_2}.\frac{x}{\sqrt{x^2+h^2}}=0\)
\(\Leftrightarrow v_1x=v_2\sqrt{x^2+d^2}\)
\(\Leftrightarrow v_1^2x^2=v_2^2\left(x^2+d^2\right)\)
\(\Leftrightarrow x=\frac{v_2d}{\sqrt{v_1^2-v_2^2}}\)
=> t=...
bạn tự thay vào r so sánh:3

Nửa quãng đường dài là :
S=\(\frac{AB}{2}=\frac{12}{2}=6\left(km\right)\)
Thời gian xe đi trong nửa quãng đường đầu là :
t1=\(\frac{S}{v_1}=\frac{6}{v_1}\left(h\right)\)
Thời gian xe đi trong nửa quãng đường sau là :
t2=\(\frac{S}{v_2}=\frac{6}{\frac{1}{2}v_1}=\frac{12}{v_1}\left(h\right)\)
Ta có : t1+t2=t
\(\Rightarrow\frac{6}{v_1}+\frac{12}{v_1}=0,5\left(h\right)\)
\(\Rightarrow\frac{18}{v_1}=0,5\)
\(\Rightarrow v_1=36\)(km/h)
\(\Rightarrow v_2=\frac{1}{2}.v_1=\frac{1}{2}.36=18\)(km/h)

Chọn A.
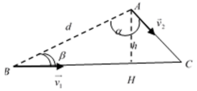
Gọi thời gian để người và xe cùng đến C là t
Ta có: AC = v 2 .t; BC = v 1 .t
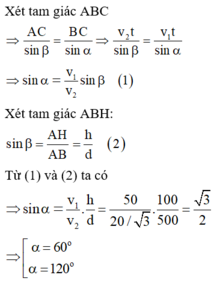

Chọn D
Gọi v 13 là vận tốc của xuồng với bờ
v 23 là vận tốc của nước với bờ bằng v 23 = 19 , 8 k m / h = 5 , 5 m / s
v 12 là vận tốc của xuồng so với dòng nước v 12 = 1 , 5 m / s
Khi xuôi dòng: v 13 = v 12 + v 23 = 7m/s ⇒ t 1 = S v 13 = 14000 7 = 2000 s
Khi ngược dòng:
v ' 13 = v 12 - v 23 = 4m/s ⇒ t 2 = S v 13 = 14000 4 = 3500 s
Vậy thời gian chuyển động của xuồng : t = t1 + t’ = 5500s.

Cho (1) là ca nô, (2) là nước, (3) là bờ sông.
(a) Trong 100s, nước chảy đưa ca nô chếch từ vị trí B đến C, nên vận tốc của dòng nước so với bờ là: \(v_{23}=\dfrac{BC}{t}=\dfrac{200}{100}=2\left(m/s\right)\)
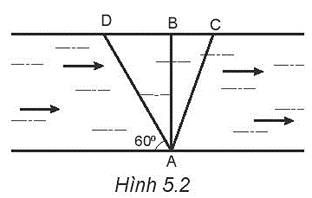
(b) Dựa vào hình vẽ, dễ thấy: \(\hat{ADB}=\alpha=60^o\).
Khi đi theo hướng \(AD:v_{12}=v_{12}';v_{23}=v_{23}'=2\left(m/s\right)\)
\(v_{23}'\) là vận tốc của dòng nước so với bờ sông, tức vecto này hướng theo hướng vector \(\overrightarrow{DB}\), \(v_{12}'\) là vận tốc của ca nô so với dòng nước, tức vecto này theo hướng vector \(\overrightarrow{AD}\).
Dựa vào hình vẽ và hệ thức lượng trong tam giác vuông: \(v_{12}'=\dfrac{v_{23}'}{cos\hat{ADB}}=\dfrac{2}{cos60^o}=4\left(m/s\right)\).
(c) Khi đi theo hướng \(AC\), vector \(\overrightarrow{v_{12}}\) hướng theo hướng vector \(\overrightarrow{AB}\)
\(\Rightarrow AB=v_{12}t=4\cdot100=400\left(m\right)\)
(d) Khi đi theo hướng \(AD\), vận tốc của thuyền so với bờ là \(v_{13}'=v_{12}'sin\hat{ADB}=4\cdot sin60^o=2\sqrt{3}\left(m/s\right)\)
Thời gian qua sông lần sau: \(t'=\dfrac{AB}{v_{13}'}=\dfrac{400}{2\sqrt{3}}\approx115,47\left(s\right)\)

Chọn B.
Gọi t và t’ lần lượt là thời gian đi xuôi dòng và thời gian đi ngược dòng.
Độ lớn vận tốc của canô đối với bờ khi đi xuôi dòng và khi đi ngược dòng lần lượt là:
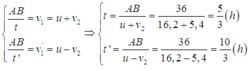
=> t + t’ = 5 (h).

Chọn A.
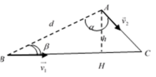
Gọi thời gian để người và xe cùng đến C là t
Ta có: AC = v2.t; BC = v1.t
Xét tam giác ABC
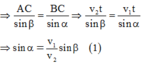
Xét tam giác ABH:
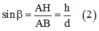
Từ (1) và (2) ta có