Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

góc F=90-30=60 độ
Xét ΔDEF vuông tại D có sin E=DF/EF
=>DF/20=1/2
=>DF=10cm
=>DE=10*căn 3(cm)

\(a,\) Áp dụng Pytago \(EF=\sqrt{DE^2+DF^2}=25\left(cm\right)\)
Áp dụng HTL:
\(\left\{{}\begin{matrix}DE^2=EH\cdot EF\\DF^2=FH\cdot EF\\DH^2=FH\cdot EH\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}EH=\dfrac{DE^2}{EF}=9\left(cm\right)\\FH=\dfrac{DF^2}{EF}=16\left(cm\right)\\DH=\sqrt{9\cdot16}=12\left(cm\right)\end{matrix}\right.\)
\(b,\sin\widehat{E}=\cos\widehat{F}=\dfrac{DF}{EF}=\dfrac{4}{5}\approx\left\{{}\begin{matrix}\sin53^0\\\cos37^0\end{matrix}\right.\\ \Rightarrow\widehat{E}\approx53^0;\widehat{F}\approx37^0\)

Xét ΔDEF vuông tại D có
\(DE=DF\cdot\cos60^0\)
\(=15\cdot\dfrac{1}{2}=7.5\left(cm\right)\)
Áp dụng định lí Pytago vào ΔDFE vuông tại D, ta được:
\(EF^2=DE^2+DF^2\)
\(\Leftrightarrow DF^2=15^2-7.5^2=\dfrac{675}{4}\)
hay \(DF=\dfrac{15\sqrt{3}}{2}\left(cm\right)\)

DE=cos E .EF
DE=0,5.15
DE=7,5cm
DF=sinE.EF
DF=\(\dfrac{\sqrt{3}}{2}.15=\dfrac{15\sqrt{3}}{2}\)
Ta có: \(\cos60^o=\dfrac{DE}{E\text{F}}=\dfrac{\text{1}}{2}\Rightarrow DE=\dfrac{E\text{F}}{2}=\dfrac{\text{1}5}{2}=7,5cm\)
Áp dụng định lí Py-ta-go vào ΔDEF vuông tại D
⇒ EF2=DE2+DF2 ⇒ DF2=EF2-DE2=152-7,52=168,75
⇒ \(DF=\dfrac{15\sqrt{3}}{2}\) cm

a: ΔDEF vuông tại D
=>\(DE^2+DF^2=EF^2\)
=>\(EF^2=0,9^2+12^2=144,81\)
=>\(EF=\sqrt{144,81}\)(cm)
Xét ΔDEF vuông tại D có \(tanE=\dfrac{DF}{DE}\)
=>\(tanE=\dfrac{12}{0,9}=\dfrac{120}{9}=\dfrac{40}{3}\)
b: Xét ΔDEF vuông tại D có
\(sinF=\dfrac{DE}{EF}=\dfrac{0.9}{\sqrt{144,81}}\)
\(cosF=\dfrac{DF}{EF}=\dfrac{12}{\sqrt{144,81}}\)
\(tanF=\dfrac{0.9}{12}=\dfrac{9}{120}=\dfrac{3}{40}\)
\(cotF=\dfrac{12}{0.9}=\dfrac{40}{3}\)

a: Xét ΔDEF có \(EF^2=DE^2+DF^2\)
nên ΔDEF vuông tại D

a) Áp dụng định lí Pytago vào ΔEDF vuông tại D, ta được:
\(EF^2=DF^2+DE^2\)
\(\Leftrightarrow DF^2=13^2-9^2=88\)
hay \(DF=2\sqrt{22}\left(cm\right)\)
Xét ΔEDF vuông tại D có
\(\sin\widehat{E}=\dfrac{DF}{EF}=\dfrac{2\sqrt{22}}{13}\)
nên \(\widehat{E}\simeq46^0\)
\(\Leftrightarrow F=44^0\)
b) Áp dụng hệ thức lượng trong tam giác vuông vào ΔDFE vuông tại D có DI là đường cao ứng với cạnh huyền EF, ta được:
\(DI\cdot EF=DF\cdot DE\)
\(\Leftrightarrow DI=\dfrac{18\sqrt{22}}{13}\left(cm\right)\)
Áp dụng định lí Pytago vào ΔDIF vuông tại I, ta được:
\(DF^2=DI^2+IF^2\)
\(\Leftrightarrow IF^2=DF^2-DI^2=\left(2\sqrt{22}\right)^2-\left(\dfrac{18\sqrt{22}}{13}\right)^2=\dfrac{7744}{169}\)
hay \(IF=\dfrac{88}{13}\left(cm\right)\)
Ta có: IE+IF=EF(I nằm giữa E và F)
nên \(IE=EF-IF=13-\dfrac{88}{13}=\dfrac{81}{13}\left(cm\right)\)
c) Xét tứ giác DMIN có
\(\widehat{NDM}=90^0\)
\(\widehat{IND}=90^0\)
\(\widehat{IMD}=90^0\)
Do đó: DMIN là hình chữ nhật(Dấu hiệu nhận biết hình chữ nhật)
Suy ra: DI=MN(Hai đường chéo của hình chữ nhật DMIN)
mà \(DI=\dfrac{18\sqrt{22}}{13}\left(cm\right)\)
nên \(MN=\dfrac{18\sqrt{22}}{13}\left(cm\right)\)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔDIE vuông tại I có IM là đường cao ứng với cạnh huyền DE, ta được:
\(DM\cdot DE=DI^2\)(1)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔDIF vuông tại I có IN là đường cao ứng với cạnh huyền DF, ta được:
\(DN\cdot DF=DI^2\)(2)
Từ (1) và (2) suy ra \(DM\cdot DE=DN\cdot DF\)

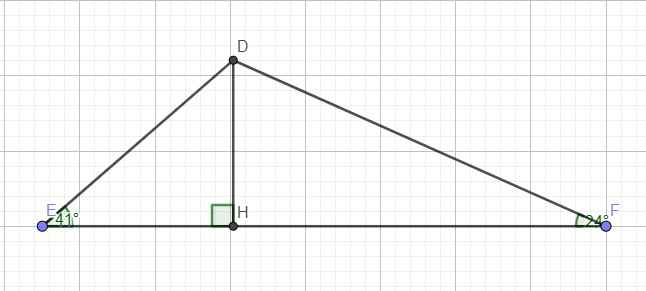
\(\widehat{E}=180^0-\left(\widehat{D}+\widehat{F}\right)=41^0\)
Trong tam giác vuông DEH:
\(cotE=\dfrac{EH}{DH}\Rightarrow EH=DH.cotE\)
Trong tam giác vuông DFH:
\(cotF=\dfrac{FH}{DH}\Rightarrow FH=DH.cotF\)
\(\Rightarrow EH+FH=\text{DH}.cotE+DH.cotF\)
\(\Leftrightarrow EF=DH\left(cotE+cotF\right)\)
\(\Rightarrow DH=\dfrac{EF}{cotE+cotF}=\dfrac{15}{cot41^0+cot24^0}\approx4,42\left(cm\right)\)
Trong tam giác vuông DEH
\(sinE=\dfrac{DH}{DE}\Rightarrow DE=\dfrac{DH}{sinE}=\dfrac{4,42}{sin41^0}\approx6,74\left(cm\right)\)