
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(x^4+6x^3+11x^2+6x+1\)
\(=x^4+3x^3+x^2+3x^3+9x^2+3x+x^2+3x+1\)
\(=\left(x^2+3x+1\right)^2\)

a) ( x 2 – 4x + 1)( x 2 – 2x + 3).
b) ( x 2 + 5x – 1)( x 2 + x – 1).

\(x^4+6x^3+x^2=x^2\left(x^2+6x+1\right)\)
\(\left(x+9\right)-\left(x+9\right)4x=\left(x+9\right)\left(1-4x\right)\)

\(x^4+6x^3+7x^2-6x+1\)
\(=x^4-2x^2+1+6x^3+9x^2-6x\)
\(=\left(x^2-1\right)^2+6x\left(x^2-1\right)+9x^2\)
\(=\left(x^2+3x-1\right)^2\)

\(a,n^3-2n^2+3n+3=n^3-n^2-n^2+n+2n-2+5\\ =\left(n-1\right)\left(n^2-n+2\right)+5\\ \Leftrightarrow n^3-2n^2+3n+3⋮\left(n-1\right)\\ \Leftrightarrow5⋮n-1\\ \Leftrightarrow n-1\in\left\{-5;-1;1;5\right\}\\ \Leftrightarrow n\in\left\{-4;0;2;6\right\}\)
\(b,\Leftrightarrow x^4+6x^3+7x^2-6x+a\\ =x^4+3x^3-x^2+3x^3+9x^2-3x-x^2-3x+1-1+a\\ =\left(x^2+3x-1\right)\left(x^2+3x-1\right)-1+a\\ =\left(x^2+3x-1\right)^2+a-1\)
Để \(x^4+6x^3+7x^2-6x+a⋮x^2+3x-1\)
\(\Leftrightarrow a-1=0\Leftrightarrow a=1\)

c: \(x^4+x^3-4x^2+x+1\)
\(=x^4-x^3+2x^3-2x^2-2x^2+2x-x+1\)
\(=\left(x-1\right)\left(x^3+2x^2-2x-1\right)\)
\(=\left(x-1\right)\left[\left(x-1\right)\left(x^2+x+1\right)+2x\left(x-1\right)\right]\)
\(=\left(x-1\right)^2\cdot\left(x^2+3x+1\right)\)

\(a,=\left(6x^3+3x^2-10x^2-5x+4x+2\right):\left(2x+1\right)\\ =\left(2x+1\right)\left(3x^2-5x+2\right):\left(2x+1\right)=3x^2-5x+2\\ b,=\left(x^4-2x^3+3x^2+x^3-2x^2+3x\right):\left(x^2-2x+3\right)\\ =\left(x^2-2x+3\right)\left(x^2+x\right):\left(x^2-2x+3\right)=x^2+x\)

\(\dfrac{x^4-6x^3+12x^2+3}{x^2-4x+1}\)
\(=\dfrac{x^4-4x^3+x^2-2x^3+8x^2-2x+2x^2-8x+2+10x+1}{x^2-4x+1}\)
\(=x^2-2x+2+\dfrac{10x+1}{x^2-4x+1}\)
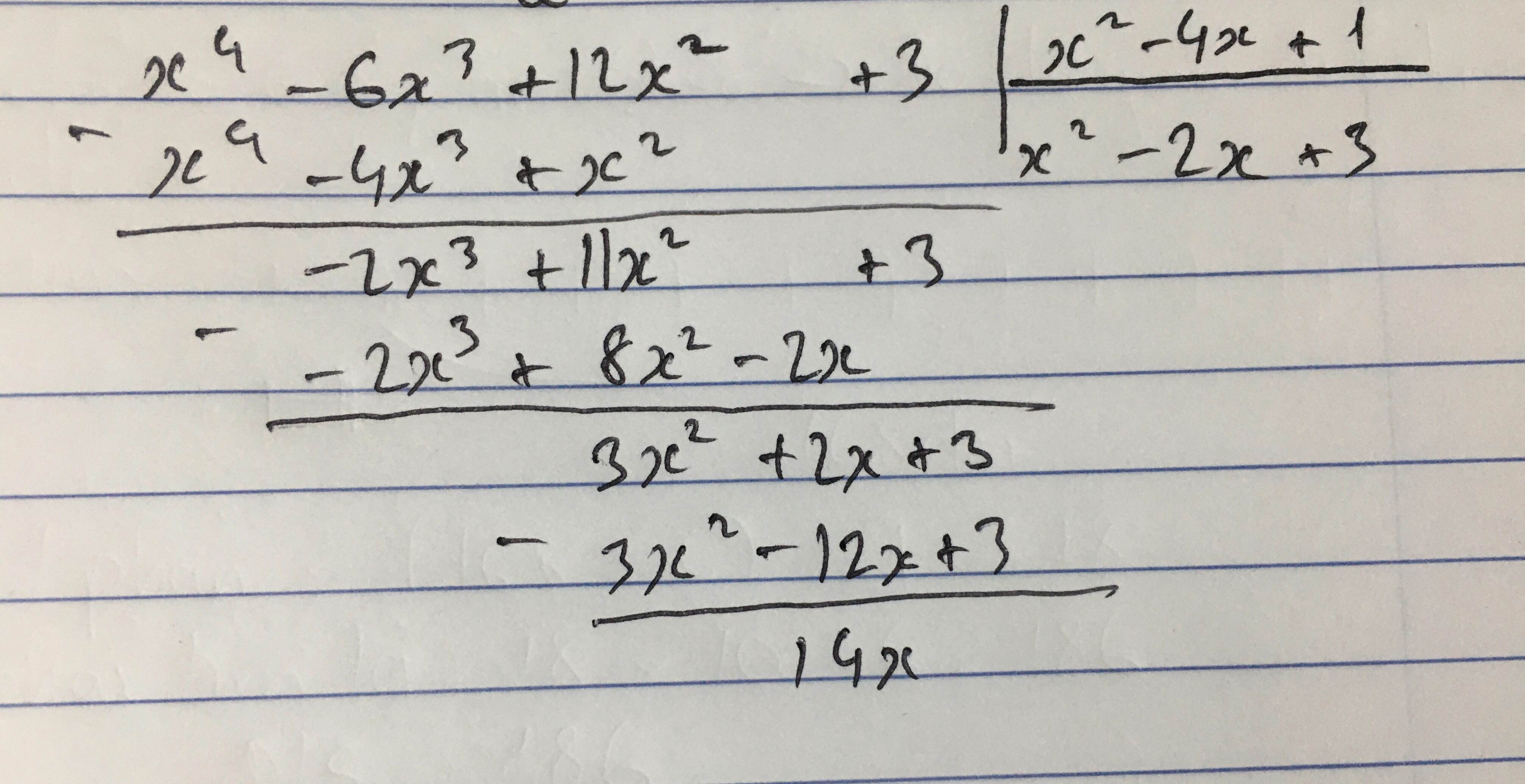
Trả lời:
\(I=x^4-6x^3+11x^2-12x+20\)
\(=x^4-6x^3+9x^2+2x^2-12x+18+2\)
\(=\left(x^4-6x^3+9x^2\right)+\left(2x^2-12x+18\right)+2\)
\(=\left[\left(x^2\right)^2-2.x^2.3x+\left(3x\right)^2\right]+2\left(x^2-6x+9\right)+2\)
\(=\left(x^2-3x\right)^2+2\left(x-3\right)^2+2\ge2\forall x\)
Dấu "=" xảy ra khi \(\hept{\begin{cases}x^2-3x=0\\x-3=0\end{cases}\Leftrightarrow\hept{\begin{cases}x=0;x=3\\x=3\end{cases}\Leftrightarrow}\hept{x=3}}\)
Vậy GTNN của I = 2 khi x = 3
\(A=x^4-6x^3+10x^2-6x+9\)
\(=x^4-6x^3+9x^2+x^2-6x+9\)
\(=\left(x^4-6x^3+9x^2\right)+\left(x^2-6x+9\right)\)
\(=\left(x^2-3x\right)^2+\left(x-3\right)^2\ge0\forall x\)
Dấu "=" xảy ra khi x = 3 (giống ý trên)
Vậy GTNN của A = 0 khi x = 3