Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

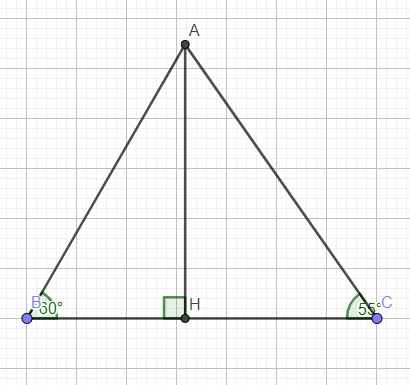
Kẻ đường cao AH ứng với BC
Trong tam giác vuông ACH:
\(sinC=\dfrac{AH}{AC}\Rightarrow AH=AC.sinC\)
\(cosC=\dfrac{CH}{AC}\Rightarrow CH=AC.cosC\)
Trong tam giác vuông ABH:
\(tanB=\dfrac{AH}{BH}\Rightarrow BH=\dfrac{AH}{tanB}=\dfrac{AC.sinC}{tanB}\)
Do đó:
\(S_{ABC}=\dfrac{1}{2}AH.BC=\dfrac{1}{2}AH\left(BH+CH\right)=\dfrac{1}{2}.4,5.sin55^0.\left(\dfrac{4,5.sin55^0}{tan60^0}+4,5.cos55^0\right)\approx8,68\left(cm^2\right)\)

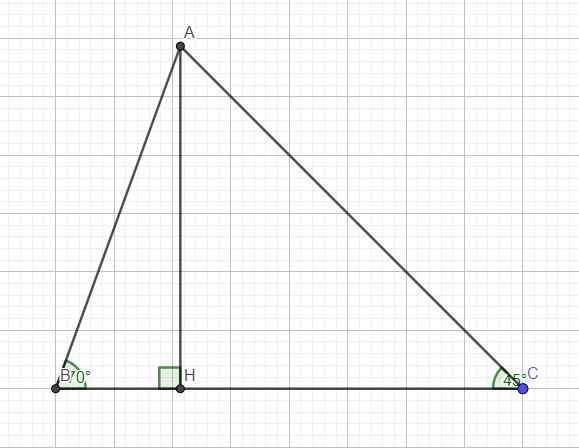
Kẻ đường cao AH ứng với BC, đặt \(CH=x\Rightarrow BH=4-x\)
Trong tam giác vuông ABH
\(tanB=\dfrac{AH}{BH}\Rightarrow AH=BH.tanB=\left(4-x\right).tan70^0\)
Trong tam giác vuông ACH:
\(tanC=\dfrac{AH}{CH}\Rightarrow AH=CH.tanC=x.tan45^0=x\)
\(\Rightarrow\left(4-x\right)tan70^0=x\)
\(\Leftrightarrow\left(1+tan70^0\right)x=4.tan70^0\)
\(\Leftrightarrow x=\dfrac{4tan70^0}{1+tan70^0}\approx2,2\left(cm\right)\)
\(\Rightarrow CH=AH=2,2\left(cm\right)\)
\(AC=\sqrt{CH^2+AH^2}=AH\sqrt{2}\approx3,1\left(cm\right)\)
\(S_{ABC}=\dfrac{1}{2}AH.BC=\dfrac{1}{2}.2,2.4=4,4\left(cm^2\right)\)

1 ,áp dụng bộ 3 pitago trong tam giác abc suy ra AC=5 cm dựa vào pitago đảo có : \(5^2+12^2\)= 13 suy ra tam giác ACD vuông tại c
S tứ giác = SABC +SADC =1/2 .3.4 +1/2. 5.12=36 cm ^2.
2,bài 2 vẽ hình lâu lém tự làm nha bn
3,
B1 minh da lam dc trc do roi nhung van cam on ban vi da giup do

Bài 2:
Xét \(\Delta ABC\)có \(\widehat{A}=90^o\)và\(AH\perp BC\)
\(\Rightarrow AH^2=HB.HC\)(Hệ thức lượng)
\(AH^2=25.64\)
\(AH=\sqrt{1600}=40cm\)
Xét \(\Delta ABH\)có\(\widehat{H}=90^o\)
\(\Rightarrow\tan B=\frac{AH}{BH}\)\(=\frac{40}{25}=\frac{8}{5}\)
\(\Rightarrow\widehat{B}\approx58^o\)
Xét \(\Delta ABC\)có \(\widehat{A}=90^o\)
\(\Rightarrow\widehat{B}+\widehat{C}=90^o\)
\(58^o+\widehat{C}=90^o\)
\(\Rightarrow\widehat{C}\approx90^o-58^o\)
\(\widehat{C}\approx32^o\)

1.
\(A+B+C=180^0\Rightarrow A=180^0-\left(B+C\right)=70^0\)
Kẻ đường cao BD
Trong tam giác vuông ABD:
\(cotA=\dfrac{AD}{BD}\Rightarrow AD=BD.cotA\)
Trong tam giác vuông BCD:
\(cotC=\dfrac{CD}{BD}\Rightarrow CD=BD.cotC\)
\(\Rightarrow AD+CD=BD.cotA+BD.cotC\)
\(\Rightarrow AC=BD.\left(cotA+cotC\right)\)
\(\Rightarrow BD=\dfrac{AC}{cotA+cotC}\)
\(\Rightarrow S_{ABC}=\dfrac{1}{2}BD.AC=\dfrac{1}{2}.\dfrac{AC^2}{cotA+cotC}=\dfrac{35^2}{2\left(cot70^0+cot50^0\right)}\approx509,1\left(cm^2\right)\)

\(\dfrac{B}{C}=\dfrac{4}{3}\Rightarrow B=\dfrac{4C}{3}\)
\(B+C=180^0-A=105^0\Rightarrow C+\dfrac{4C}{3}=105^0\Rightarrow C=45^0\) \(\Rightarrow B=60^0\)
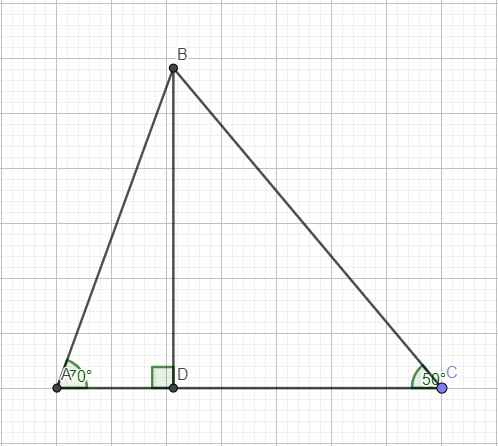
Kẻ đường cao AD ứng với BC (do 2 góc B và C đều nhọn nên D nằm giữa B và C)
Trong tam giác vuông ABD:
\(sinB=\dfrac{AD}{AB}\Rightarrow AD=AB.sinB=10,6.sin60^0\approx9,2\left(cm\right)\)
\(cosB=\dfrac{BD}{AB}\Rightarrow BD=AB.cosB=10,6.cos60^0=5,3\left(cm\right)\)
Trong tam giác vuông ACD:
\(tanC=\dfrac{AD}{CD}\Rightarrow CD=AD.tanC=9,2.tan45^0=9,2\left(cm\right)\)
\(sinC=\dfrac{AD}{AC}\Rightarrow AC=\dfrac{AD}{sinC}=\dfrac{9,2}{sin45^0}\approx13\left(cm\right)\)
\(BC=BD+CD=5,3+9,2=14,5\left(cm\right)\)
\(S_{ABC}=\dfrac{1}{2}AD.BC=\dfrac{1}{2}.9,2.14,5=66,7\left(cm^2\right)\)

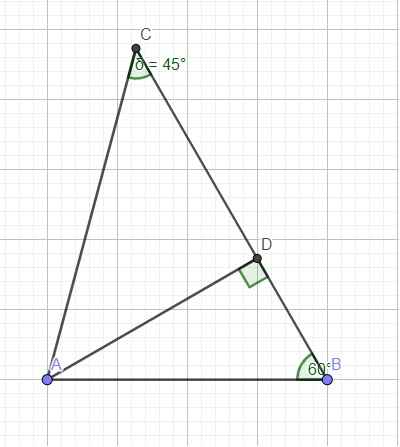
Có \(\widehat{B}=180^0-105^0-30^0=45^0\)
Kẻ AH vuông góc với BC
\(\Rightarrow\Delta ABH\) là tam giác vuông cân tại A
\(\Rightarrow AH=BH\)
Có \(tanC=\dfrac{AH}{HC}\Leftrightarrow HC=\dfrac{AH}{tan30^0}=\sqrt{3}AH\)
\(\Rightarrow BH+CH=AH+\sqrt{3}AH\Leftrightarrow BC=\left(1+\sqrt{3}\right)AH\)\(\Leftrightarrow AH=\dfrac{BC}{1+\sqrt{3}}=\dfrac{2}{1+\sqrt{3}}\)
\(S_{ABC}=\dfrac{1}{2}AH.BC=\dfrac{1}{2}.\dfrac{2}{1+\sqrt{3}}.2=\dfrac{2}{1+\sqrt{3}}\) (cm2)
Vậy...