Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a) sửa đề => đường trung trực
ta có tg ABC cân tại A
M là trung điểm của BC
=> AM là đường trung trực của BC
=> AM là đường pg của tg ABC (t/c tg cân )
=> gBAM = gCAM hay gEAM = gFAM
xét tg AME và tg AMF có
gEAM = gFAM (cmt)
AM chung
gAEM = gAFM (=90o)
=> tg AME = tgAMF (cạnh huyền góc nhọn )
=> ME = MF (2 cạnh t/ư )
Bài làm :
a) Xét tam giác BEM và tam giác CFM
Ta có: BM = MC ( vì M là trung điểm của BC)
M là góc chung
Do đó : tam giác BEM=CFM( cạnh huyền- góc nhọn)
b) Bạn ghi chưa hết đề nên mik ko hiểu
sorry 
Mình xin phép sửa đề:
Cho tam giac ABC cân tại A, M là trung điểm của BC, ME vuông góc với AB, MF vuông góc với AC. Chứng minh ME = MF và AM là đường trung trực của EF.
\(\text {(1)}\)
Xét Tam giác `ABM` và Tam giác `ACM` có:
`AB = AC (\text {Tam giác ABC cân tại A})`
\(\widehat {B}= \widehat {C}(\text {Tam giác ABC cân tại A})\)
`MB = MC (\text {M là trung điểm của BC})`
`=> \text {Tam giác ABM = Tam giác ACM (c-g-c)}`
`->`\(\widehat {BAM}=\widehat {CAM} (\text {2 góc tương ứng})\)
Xét Tam giác `AEM` và Tam giác `AFM` có:
`\text {AM chung}`
\(\widehat{BAM}=\widehat{CAM} (CMT)\)
\(\widehat{AEM}=\widehat{AFM} (=90^0)\)
`=> \text {Tam giác AEM = Tam giác AFM (ch-gn)}`
`-> ME = MF (2 cạnh tương ứng)`
\(\left(2\right)\)
Gọi `I` là giao điểm của `AM` và `EF`
C1:
Vì Tam giác `AEM =` Tam giác `AFM (\text {Theo CMT})`
`-> AE = AF (\text {2 cạnh tương ứng})`
Xét Tam giác `AEI` và Tam giác `AFI` có:
`AE = AF (CMT)`
\(\widehat{EAI}=\widehat{FAI} (\text {Theo CMT})\)
`\text {AI chung}`
`=> \text {Tam giác AEI = Tam giác AFI (c-g-c)}`
`-> IE = IF (\text {2 cạnh tương ứng})`
`->`\(\widehat{AIE}=\widehat{AIF} (\text {2 góc tương ứng})\)
Mà `2` góc này nằm ở vị trí kề bù
`->`\(\widehat{AIE}+\widehat{AIF}=180^0\)
`->`\(\widehat{AIE}=\widehat{AIF}=\)`180/2=90^0`
`-> \text {AI} \bot \text {EF}`
\(\text{Ta có: }\left\{{}\begin{matrix}\text{IE = IF }\\\text{AI}\perp\text{EF}\end{matrix}\right.\)
`-> \text {AI là đường trung trực của EF}`
`-> \text {AM là đường trung trực của EF}`
C2 (nếu bạn đã học về tính chất của tam giác cân với các đường Trung Tuyến, Đường Cao, Đường Trung Trực) :
Ta có:
AM vừa là đường phân giác, vừa là đường trung tuyến
`*` Theo tính chất của tam giác cân
`-> \text {AM là đường trung trực của EF (đpcm)}`
`@`\(\text{dnammv}\)
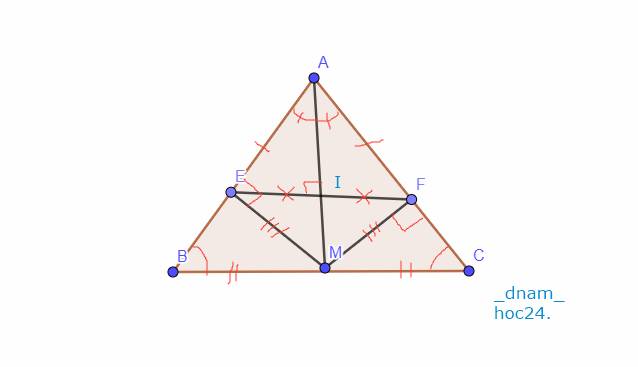
Sửa đề: Đường trung tuyến AM
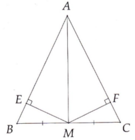
a: Xét ΔBEM vuông tại E và ΔCFM vuông tại F có
MB=MC
góc B=góc C
=>ΔBEM=ΔCFM
b: ΔBEM=ΔCFM
=>BE=CF và ME=MF
AE+EB=AB
AF+FC=AC
mà EB=FC và AB=AC
nên AE=AF
mà ME=MF
nên AM là trung trực của EF
c: Xét ΔABC có AE/AB=AF/AC
nên EF//BC
b) ta có tam giác ABC cân
=> \(\widehat{B}=\widehat{C}=180-\widehat{A}\) (1)
mà AM là trung tuyến => AM cx là phân giác và AM cx là đường cao (t/c tam giác cân)
=>\(\widehat{A1}=\widehat{A2}\)
xét tam giác AEM và tam giác AfM
có AM chung
\(\widehat{E}=\widehat{F}\)=90o
\(\widehat{A1}=\widehat{A2}\)
=> tam giác AEM =tam giác AFM (CH-GN)
=> AE =AC (2 cạnh tương ứng)
=> tam giác AEF cân ở \(\widehat{A}\)
=> \(\widehat{E}=\widehat{F}=180-\widehat{A}\) (2)
từ 1 và 2 =>\(\widehat{E}=\widehat{B}\) mà 2 góc ở vt đồng vị
=> EF // BC
mà AM ⊥ BC
=> EF ⊥ AM
=> AM là trung trực của EF (t/c tam giác cân)
a) xét ΔABM và ΔACM có
góc B = góc C
AB = AC ( ΔABC cân tại A )
BM=CM ( tính chất các đường của Δ cân từ đỉnh )
=> ΔABM = ΔACM
b) xét ΔBME và ΔCMF có
góc B bằng góc C
BM=CM
=> ΔBME=ΔCMF ( cạnh huyền góc nhọn )
=> FM = EM
=> ΔEMF cân tại M
c) gọi giao của EF và AM là O
ta có BE = CF => AE=AF
=> ΔAEF cân tại A
ta có AM là tia phân giác của góc A
mà O nằm trên AM suy ra AO cũng là tia phân giác của góc A
ta lại có ΔAEF cân tại A
suy ra AO vuông góc với EF
suy ra AM vuông góc với EF
xét ΔAEF và ΔABC có
EF và BC đều cùng vuông góc với AM => EF // BC
a) Xét ΔABM và ΔACM có
AB=AC(ΔABC cân tại A)
AM chung
BM=CM(M là trung điểm của BC)
Do đó: ΔABM=ΔACM(c-c-c)
b) Xét ΔEMB vuông tại E và ΔFMC vuông tại F có
BM=CM(M là trung điểm của BC)
\(\widehat{EBM}=\widehat{FCM}\)(hai góc ở đáy của ΔABC cân tại A)
Do đó: ΔEMB=ΔFMC(Cạnh huyền-góc nhọn)
Suy ra: ME=MF(hai cạnh tương ứng)
Xét ΔEMF có ME=MF(cmt)
nên ΔEMF cân tại M(Định nghĩa tam giác cân)
Tham Khảo :
Xét `△BEM` và `△ CFM`:
\(\widehat{MEB}=\widehat{CFM}\)
`BM = MC`
\(\widehat{EBM}=\widehat{FCM}\)
`=>△BEM = △ CFM`
`=> BE = FC`
Ta có:
` AB = AE + EB`
` AC = AF + FC`
Mà `AB = AC` (vì △ABC cân tại A)
`EB = FC (cmt)`
`=> AE = AF`
`=>` △AEF` cân tại A
Xét `△AEM` và `△AFM` có:
AE = AF
\(\widehat{AEM}=\widehat{AFM}\)
AM cạnh chung
`=> △AEM =△AFM`
`=>` \(\widehat{EAM}=\widehat{FAM}\)
`=> AM là đường phân giác
Xét △AEF cân tại A có:
AM là đường phân giác
`=>` AM là trung trực của BC
b) Ta có: △AEM =△AFM
=> ME = MF
Xét △AEF cân tại A có:
AM là đường phân giác
=> AM là đường trung trực của EF