Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1. Ta có :
B(x)=x2+5 mà x2 luôn > hoặc = 0
và 5>0
=>x2+5 luôn > 0
Vậy đa thức B(x) không có nghiệm
Ta có : B ( x ) = x^2 + 5
Mà x^2 lớn hơn hoặc bằng 0
5 > 0
Suy ra x^2 + 5 > 0
Suy ra đa thức B ( x ) không có nghiệm

Bài 1
c) 2.3ˣ.3² = 18
3ˣ⁺² = 18 : 2
3ˣ⁺² = 9
3ˣ⁺² = 3²
x + 2 = 2
x = 2 - 2
x = 0
Bài 2
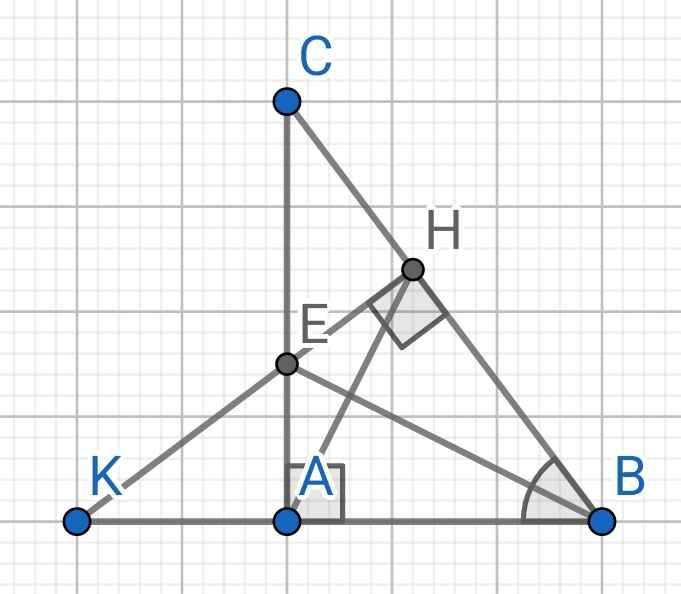 a) Do BE là tia phân giác của ∠ABC (gt)
a) Do BE là tia phân giác của ∠ABC (gt)
⇒ ∠ABE = ∠HBE
Xét hai tam giác vuông: ∆ABE và ∆HBE có:
BE là cạnh chung
∠ABE = ∠HBE (cmt)
⇒ ∆ABE = ∆HBE (cạnh huyền - góc nhọn)
b) Gọi D là giao điểm của AH và BE
Do ∆ABE = ∆HBE (cmt)
⇒ AB = HB (hai cạnh tương ứng)
Xét ∆ABD và ∆HBD có:
BD là cạnh chung
∠ABD = ∠HBD (BE là phân giác của ∠ABC)
AB = HB (cmt)
⇒ ∆ABD = ∆HBD (c-g-c)
⇒ AD = HD (hai cạnh tương ứng)
⇒ D là trung điểm của AH (1)
Lại do ∆ABD = ∆HBD (cmt)
⇒ ∠ADB = ∠HDB (hai góc tương ứng)
Mà ∠ADB + ∠HDB = 180⁰ (kề bù)
⇒ ∠ADB = ∠HDB = 180⁰ : 2
= 90⁰ (2)
Từ (1) và (2) ⇒ BD là đường trung trực của AH
Hay BE là đường trung trực của AH
c) Do ∆ABE = ∆HBE (cmt)
⇒ AE = HE (hai cạnh tương ứng)
Xét hai tam giác vuông: ∆AEK và ∆HEC có:
AE = HE (cmt)
∠AEK = ∠HEC (đối đỉnh)
⇒ ∆AEK = ∆HEC (cạnh góc vuông - góc nhọn kề)
⇒ EK = EC (hai cạnh tương ứng)

\(A\left(x\right)=2x^2-x^3+x-3\)
\(B\left(x\right)=x^3-x^2+3-3x\)
a, Ta có : \(P\left(x\right)=A\left(x\right)+B\left(x\right)=2x^2-x^3+x-3+x^3-x^2+3-3x\)
\(=x^2-2x\)
b, Đề khs hiểu thế, đã là 1 đa thức thì luôn đặt đa thức ''='' 0 thôi :v
Đặt \(P\left(x\right)=x^2-2x=0\)
\(\Leftrightarrow x\left(x-2\right)=0\Leftrightarrow\orbr{\begin{cases}x=0\\x=2\end{cases}}\)
Vậy đa thức có nghiệm là 0;2
c, \(Q\left(x\right)=5x^2+a^2+ax\)
Ta có : \(Q\left(-1\right)=5\left(-1\right)^2+a^2+a\left(-1\right)=0\)
\(\Leftrightarrow5+a^2-a=0\)(cùy, ko nốt đc)
Suy ra : Vô nghiệm Vậy đa thức ko có nghiệm.

Diễn giải:
- Khi cộng, trừ số thập phân ta tiến hành cộng hoặc trừ các phần tương ứng của các số đó.
Ví dụ 1:
Tính 0,25 + 2,5 ta làm như sau: 5 + 0 = 5 , 2 + 5 =7, 0 + 2 = 2. Vậy 0,25 + 2,5 = 2.75
Tính 8,6 - 2,7 ta làm như sau: 6 - 7 không trừ được ta lấy 16 - 7 = 9, tiếp tục 8 - 2 trừ thêm 1 nữa tức là 8 -3 = 5. Vậy 8,6 - 2,7 = 5,9
- Với phép nhân, chia các số thập phân ta cần viết chúng dưới dạng phân số.
Bài 4:
\(a^2+b^2+c^2=ab+bc+ca\)
\(\Leftrightarrow2\left(a^2+b^2+c^2\right)=2\left(ab+bc+ca\right)\)
\(\Leftrightarrow2a^2+2b^2+2c^2=2ab+2bc+2ca\)
\(\Leftrightarrow2a^2+2b^2+2c^2-2ab-2bc-2ca=0\)
\(\Leftrightarrow a^2+a^2+b^2+b^2+c^2+c^2-2ab-2bc-2ca=0\)
\(\Leftrightarrow\left(a^2+b^2-2ab\right)+\left(b^2+c^2-2bc\right)+\left(c^2+a^2-2ca\right)=0\)
\(\Leftrightarrow\left(a-b\right)^2+\left(b-c\right)^2+\left(c-a\right)^2=0\)
Vì \(\left(a-b\right)^2\ge0;\left(b-c\right)^2\ge0;\left(c-a\right)^2\ge0\) (với mọi a;b;c)
\(\Rightarrow\left(a-b\right)^2+\left(b-c\right)^2+\left(c-a\right)^2\ge0\)
Dấu "=" xảy ra \(\Leftrightarrow\left(a-b\right)^2=0;\left(b-c\right)^2=0;\left(c-a\right)^2=0\)
<=>a=b;b=c;c=a
<=>a=b=c(đpcm)
đè thi hok kì thì phải tự lm chứ