Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi x là số đơn vị sản phẩm loại I, y là số đơn vị sản phẩm loại II sản xuất ra.
Như vậy tiền lãi có được là L = 3x + 5y (nghìn đồng).
Theo đề bài: Nhóm A cần 2x + 2y máy;
Nhóm B cần 0x + 2y máy;
Nhóm C cần 2x + 4y máy;
Vì số máy tối đa ở nhóm A là 10 máy, nhóm B là 4 máy, nhóm C là 12 máy nên x, y phải thỏa mãn hệ bất phương trình: 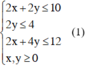
Khi đó bài toán trở thành: trong các nghiệm của hệ bất phương trình (1) thì nghiệm (x = xo; y = yo) nào cho L = 3x + 5y lớn nhất.
Miền nghiệm của hệ bất phương trình (1) là ngũ giác ABCDE kể cả miền trong.
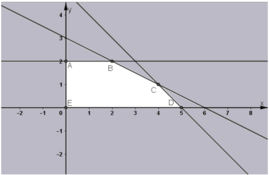
Ta có: L đạt giá trị lớn nhất tại một trong các đỉnh của ngũ giác ABCDE.
Tính giá trị của biểu thức L = 3x + 5y tại các đỉnh ta được:
Tại đỉnh A(0;2), L = 10
Tại đỉnh B(2; 2), L = 16
Tại đỉnh C(4; 1), L = 17
Tại đỉnh D(5; 0), L = 15
Tại đỉnh E(0; 0), L = 0.
Do đó, L = 3x + 5y lớn nhất là 17 (nghìn đồng) khi: x = 4; y = 1
Vậy để có tiền lãi cao nhất, cần sản xuất 4 đơn vị sản phẩm loại I và 1 đơn vị sản phẩm loại II.

Phân số chỉ số mét đường ngày thứ ba sửa được là:
\(1-\left(\frac{3}{8}+\frac{1}{3}\right)=\frac{7}{24}\)
Số mét đoạn đường dài là:
\(14\div\frac{7}{24}=48\) (m)
Đáp số: 48 mét
Chúc bạn học tốt![]()
Phân số chỉ số đoạn đường đội công dân sửa được trong hai ngày:
3/8+1/3=17/24 (mét)
Phân số chỉ số đoạn đường đội công nhân sửa trong ngày thứ 3 :
1-17/24=7/24(mét)
Số đoạn dài là:
14:7/24=48 (mét)
Đáp số:48 mét

Gọi số tiền của 3 người lần lượt là a, b và c.
Áp dụng tính chất của day tỉ số bằng nhau, ta có:
\(\frac{a}{2}=\frac{b}{3}=\frac{c}{4}=\frac{a+b+c}{2+3+4}=\frac{18}{9}=2\)
\(\frac{a}{2}=2\Rightarrow a=4\)
\(\frac{b}{3}=2\Rightarrow b=6\)
\(\frac{c}{4}=2\Rightarrow c=8\)
Vậy số tiền của 3 người lần lượt là 4 triệu, 6 triệu và 8 triệu.

- Gọi thời gian đội 1 làm xong công việc là x ( giờ , x > 4 )
- Gọi thời gian đội 2 làm xong công việc là y ( giờ , y > 4 )
Theo đề bài nếu mỗi đội làm một mình xong công việc đó, đội 1 cần tời gian ít hơn so với đội 2 là 6h nên ta có phương trình :
\(-x+y=6\left(I\right)\)
- Số công việc đội 1 làm trong1 giờ là : \(\frac{1}{x}\) ( công việc )
- Số công việc đội 2 làm trong1 giờ là : \(\frac{1}{y}\) ( công việc )
- Số công việc 2 đội làm trong1 giờ là : \(\frac{1}{4}\) ( công việc )
Theo đề bài hai đội công nhân cùng làm một công việc thì xong trong 4h nên ta có phương trình : \(\frac{1}{x}+\frac{1}{y}=\frac{1}{4}\left(II\right)\)
- Từ ( I ) và ( II ) ta có hệ phương trình : \(\left\{{}\begin{matrix}y-x=6\\\frac{1}{x}+\frac{1}{y}=\frac{1}{4}\end{matrix}\right.\)
=> \(\left\{{}\begin{matrix}y=6+x\\\frac{1}{x}+\frac{1}{x+6}=\frac{1}{4}\end{matrix}\right.\)
=> \(\left\{{}\begin{matrix}y=6+x\\\frac{x+6}{x\left(x+6\right)}+\frac{x}{x\left(x+6\right)}=\frac{1}{4}\end{matrix}\right.\)
=> \(\left\{{}\begin{matrix}y=6+x\\4\left(2x+6\right)=x\left(x+6\right)\end{matrix}\right.\)
=> \(\left\{{}\begin{matrix}y=6+x\\8x+24-x^2-6x=0\end{matrix}\right.\)
=> \(\left\{{}\begin{matrix}y=6+x\\\left(x+4\right)\left(x-6\right)=0\end{matrix}\right.\)
=> \(\left\{{}\begin{matrix}y=6+x\\x-6=0\end{matrix}\right.\)
=> \(\left\{{}\begin{matrix}y=6+6=12\\x=6\end{matrix}\right.\) ( TM )
Vậy để làm xong công việc người thứ nhất cần 6 giờ, người thứ hai cần 12 giờ .

Gọi x là số đơn vị sản phẩm loại I, y là số đơn vị sản phẩm loại II được nhà máy lập kế hoạch sản xuất. Khi đó số lãi nhà máy nhân được là P = 3x + 5y (nghìn đồng).
Các đại lượng x, y phải thỏa mãn các điều kiện sau:
(I)
(II)
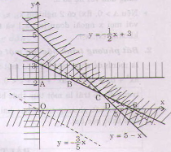
Miền nghiệm của hệ bất phương trình (II) là đa giác OABCD (kể cả biên).
Biểu thức F = 3x + 5y đạt giá trị lớn nhất khi (x; y) là tọa độ đỉnh C.
(Từ 3x + 5y = 0 => y = Các đường thẳng qua các đỉnh của OABCD và song song với đường y =
cát Oy tại điểm có tung độ lớn nhất là đường thẳng qua đỉnh C).
Phương trình hoành độ điểm C: 5 - x = <=> x = 4.
Suy ra tung độ điểm C là yc = 5 - 4 = 1. Tọa độ C(4; 1). Vậy trong các điều kiện cho phép của nhà máy, nếu sản xuất 4 đơn vị sản phẩm loại I và 1 đơn vị sản phẩm đơn vị loại II thì tổng số tiền lãi lớn nhất bằng:
Fc = 3.4 + 5.1 = 17 nghìn đồng.

Sửa đề: Số công nhân của 3 đội là 39 người
Gọi số công nhân của đội 1,2,3 lần lượt là a,b,c
Theo đề, ta có: 2a=3b=4c
=>a/6=b/4=c/3
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{a}{6}=\dfrac{b}{4}=\dfrac{c}{3}=\dfrac{a+b+c}{6+4+3}=\dfrac{39}{13}=3\)
=>a=18; b=12; c=9
