Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét tứ giác ABKH có
AB//HK
AB=HK
Do đó: ABKH là hình bình hành
mà \(\widehat{AHK}=90^0\)
nên ABKH là hình chữ nhật

TỨ GIÁC ABHK LÀ HCN DẤU HIỆU 1
B)
TAM GIÁC AHD= TAM GIÁC BCK (CH-CGV)VÌ
GÓC H = GÓC K ( CÙNG BẰNG 90 ĐỘ)
AH=AK(ABHK LÀ HCN)
AD=BC(ABCD LÀ HÌNH THANG CÂN)
SUY RA DH=KC ( HAI CẠNH TƯƠNG ỨNG)

a: Xét tứ giác ABKH có
AB//HK
AH//BK
Do đó: ABKH là hình bình hành
mà \(\widehat{AHK}=90^0\)
nên ABKH là hình chữ nhật

Bài 8:
a: Xét ΔDBC có
E là trung điểm của BD
M là trung điểm của BC
Do đó: EM là đường trung bình của ΔDBC
Suy ra: EM//DC
b: Xét ΔAEM có
D là trung điểm của AE
DI//EM
Do đó: I là trung điểm của AM
Bài 5:
Xét ΔABC có
\(\dfrac{AE}{EB}=\dfrac{AD}{DC}\left(=1\right)\)
Do đó: DE//BC
Xét tứ giác BEDC có DE//BC
nên BEDC là hình thang
mà \(\widehat{EBC}=\widehat{DCB}\)
nên BEDC là hình thang cân

a) Chứng minh
DADH = DBCK (ch-gnh)
Þ DH = CK
Vận dụng nhận xét hình thang ABKH (AB//KH) có AH//BK Þ AB = HK
b) Vậy D H = C D − A B 2
c) DH = 4cm, AH = 3cm; SABCD = 30cm2
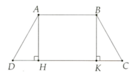

b)Xét tam giác ADH và tam giác BCK có:
AH=BK,AD=BC,góc AHD=góc BKC=90^0
=>Tam giác ADH=tam giác BCK
=>DH=CK(đpcm)
c)Do E là điểm đối xứng của D qua H nên:
góc AED=góc ADH=góc BCK
=>AE//BC
Kết hợp AB//EC
=>ABCE là hình bình hành
1) Vì AH\(\perp\)DC
BK\(\perp\)DC
=> AH//BK
Mà BAH + AHK = 180° ( trong cùng phía)
=> BAH = 90°
Mà ABK + BKH = 180° ( trong cùng phía)
=> ABK = 90°
Mà BAH = AHK = 90°
Mà 2 góc này ở vị trí trong cùng phía
=> AB//HK
=> ABKH là hình thang cân
=> ABKH là hình thang cân
=> AB = HK , AH = BK
b) Vì ABCD là hình thang cân
=> AD = BC
=> ADC = BCD
Xét ∆ vuông AHD và ∆ vuông BKC ta có :
AD = BC
ADC = BCD
=> ∆AHD = ∆BKC (ch-gn)
Mà DH = KC ( tương ứng)
c) Ta có :
DH + HK + KC = DC
Mà HK = AB
=> DH + AB + KC = DC
DH + KC = DC - AB
Mà DH = KC
=> DH = \(\frac{1}{2}\)( CD - AB )
thêm hình cho bài nó hoàn chỉnh :))