Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

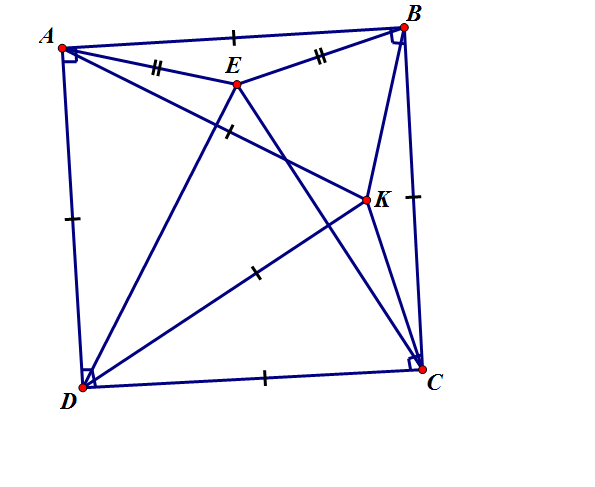
Phía trong của hình vuông ABCD ta dựng tam giác đều ADK. Ta có AD = AK = DK.
\(\widehat{DAK}=90^o-\widehat{KAD}=30^o\).
Do AB = AK (cùng bằng AD) nên tam giác BAK cân tại A.
Suy ra \(\widehat{ABK}=\widehat{AKB}=\frac{180^o-\widehat{BAK}}{2}=75^o\).
Suy ra \(\widehat{BKC}=90^o-\widehat{ABK}=15^o\).
Tương tự ta cũng có \(\widehat{KDC}=30^o,\widehat{DCK}=75^o,\widehat{KCB}=15^o\).
Dễ dàng chứng minh được \(\Delta ABE=\Delta BKC\left(g.c.g\right)\) nên AE = BE = BK = KC.
Từ đó ta chứng minh được \(\Delta AED=\Delta CDK\left(c.g.c\right)\).
Suy ra \(\widehat{ADE}=\widehat{KDC}=30^o\).
Suy ra tam giác CDE đều.

BN CÓ THỂ GIẢI THEO 1 TRONG 3 CÁCH SAU
- CÁCH 1:
- vẽ tam giác đều ADK(K và B cùng phía với AD)
- =>ˆDAKDAK^=60∘60∘=>ˆKABKAB^=90∘90∘-60∘=30∘60∘=30∘.
- ΔABKΔABK cân tại A=>ˆABK=75∘ABK^=75∘=>KBC=90∘−75∘=15∘90∘−75∘=15∘
- tương tự
- ΔDKCΔDKCcân tại D=>ˆDKC=180∘−30∘2=75∘DKC^=180∘−30∘2=75∘=>ˆKCB=15∘KCB^=15∘
- có ΔAEB=ΔBKCΔAEB=ΔBKC(g.c.g)=>AE=BK=KCΔADE=ΔKDCΔADE=ΔKDC(c.g.c)
- =>DE=DC(1), ˆADE=ˆKDC=30∘ADE^=KDC^=30∘=>ˆEDC=60∘EDC^=60∘ (2)
(1),(2)→ΔEDC đều
- CÁCH 2
- Dựng tam giác đều DME (M trong tam giác ADE)
- MDA=15∘⇒ΔADM=ΔCDE(c.g.c)⇒AM=CE=DE=DM⇒ˆMAD=15∘⇒ˆAMD=150∘⇒ˆAME=150∘⇒ΔAMD=ΔAME(c.g.c)⇒AE=AD=AB⇒MDA^=15∘⇒ΔADM=ΔCDE(c.g.c)⇒AM=CE=DE=DM⇒MAD^=15∘⇒AMD^=150∘⇒AME^=150∘⇒ΔAMD=ΔAME(c.g.c)⇒AE=AD=AB
- Tính được ˆBAE=60∘→BAE^=60∘→ tam giác ABE là tam giác đều
- CÁCH 3
:-Lấy E' trong hình vuông ABCD sao cho tam giác DCE' đều.
-Ta có: DE'=DA và góc ADE'= 30 độ.
=> góc DAE'= 75 độ. Và có góc DAB=90 độ.
=> góc BAE'= 15 độ.
-Chứng minh tương tự, ta có góc ABE'=15 độ.
Suy ra điểm E trùng với E'.
Vậy tam giác DEC đều.
NHỚ TK MK NHA,

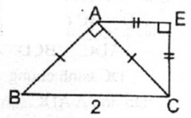
Tam giác ABC vuông cân tại A
⇒ ∠ (ACB) = 45 0
Tam giác EAC vuông cân tại E
⇒ ∠ (EAC) = 45 0
Suy ra: ∠ (ACB) = ∠ (EAC)
⇒ AE // BC (vì có cặp góc ở vị trí so le trong bằng nhau)
nên tứ giác AECB là hình thang có ∠ E = 90 0 . Vậy AECB là hình thang vuông

Bài 2:
kẻ hình thang ABCD
kẻ 2 đường cao AH và BK nối B với H
xét tam giác ABH và tam giác KBH
có ^ABH = ^KBH ( 2gocs so le trong )
HB chung
=> tam giác ABH = tam giác KBH (cạnh huyền +góc nhọn )
=> AB =HK ( 2 cạnh tương ứng )
xét tam giác BKC có BC>KC ( trong tam giác vuông cạnh huyền là cạnh lớn nhất )(1)
xét tam giác AHD có AD>HD (trong tam giác vuông cạnh huyền là cạnh lớn nhất)(2)
từ (1) và (2) => BC+AD >KC+HD
ta lại có DH+DK +HK =DC
mà AB=HK (C/m )
=> DH+DK+AB =dc
ta có DC-AB = DH+DK+AB-AB= DH+DK
mà DH+DK<BC+AD(c/m)
=>DC -AB< BC+AD
vậy tổng hai cạnh bên của hình thang lớn hơn hiệu hai đáy