Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Tại t = 2s vật đi qua vị trí x = 3 2 A = 2 , 5 3 c m theo chiều âm.
→ Biểu diễn các vị trí tương ứng trên đường tròn.
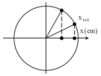
+ Khoảng thời gian ∆ t tương ứng với góc quét
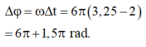
+ Ứng với góc quét 6 π vật đi qua vị trí thỏa mãn yêu cầu bài toán 3 lần, với 1 , 5 π vật chưa đi qua vị trí bài toán yêu cầu.
→ Vậy có tất cả 3 lần.
Đáp án A

Đối với những bài tìm quãng đường trong khoảng từ t1 đến t2 thì bạn lấy t2-t1 rồi phân tích chúng ra thành \(\left[{}\begin{matrix}t_2-t_1=n.\dfrac{T}{2}+t'\\t_2-t_1=n.T+t''\end{matrix}\right.\) để dễ dàng tính. Tuyệt đối ko được phân tích thành T/4 hay T/3; T/6;T/v.v. bởi nó ko luôn đúng trong các trường hợp, nếu bạn cần mình sẽ lấy ví dụ cụ thể. Giờ mình sẽ áp dụng vô bài của bạn
\(t_2-t_1=\dfrac{17}{3}-2=\dfrac{11}{3}\left(s\right)=3+\dfrac{2}{3}\)
\(T=\dfrac{2\pi}{\pi}=2s\Rightarrow t_2-t_1=3.\dfrac{T}{2}+\dfrac{2}{3}\)
Trong 3T/2 vật đi được quãng đường là: \(S_1=6A=30\left(cm\right)\)
Tại thời điểm t1=2s, lúc này vật đã quay được:\(\varphi=2\pi\left(rad\right)\) nghĩa là quay về vị trí ban đầu
Trong 2/3 s vật quay được góc: \(\varphi=\dfrac{2}{3}\pi\left(rad\right)\)
Sử dụng đường tròn lượng giác, vật ở vị trí có pha là 2pi/3, quay được góc 2pi/3 thì lúc này vật có li độ là: \(x=-2,5\left(cm\right)\)
Nghĩa là vật đi từ vị trí có li độ x1=-2,5 theo chiều âm đến vị trí có li độ x2=-2,5 theo chiều dương, vậy quãng đường vật đi được là: \(S_2=\dfrac{A}{2}+\dfrac{A}{2}=A=5\left(cm\right)\)
Vậy tổng quãng đường vật đi được là: \(S=S_1+S_2=35\left(cm\right)\)

Đáp án A
+ Tại t = 2 s vật đi qua vị trí x = 3 2 A = 2 , 5 3 cm theo chiều âm.
→ Biểu diễn các vị trí tương ứng trên đường tròn.
+ Khoảng thời gian Δt tương ứng với góc quét
Δφ = ωΔt = 6 π 3 , 25 − 2 = 6 π + 1 , 5 π rad.
+ Ứng với góc quét 6π vật đi qua vị trí thoãn mãn yêu cầu bài toán 3 lần, với 1,5π vật chưa đi qua vị trí bài toán yêu cầu.
→ Vậy có tất cả 3 lần.

Chọn B
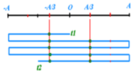
+ Khi Wđ = 8Wt => x = ±A/3 = ±4/3 cm và T = 2s.
+ t1 = 1/6s => x1 = 0cm; t2 = 13/3 s => x2 = -2cm.
![]()
+ Ta thấy cứ 1T vật đi qua 2 vị trí x = ±4/3 cm tất cả 4 lần.
=> Sau 2T vật đi qua 8 lần.
Khi đó, vật ở vị trí x1 = 0cm (VTCB) đi tiếp lượng T/12 đến x2 = -2cm qua vị trí x = -4/3 cm một lần nữa. Ta có hình ảnh minh họa hình trên.
=> Tổng cộng vật đi qua vị trí động năng bằng 8 lần thế năng 9 lần.

Để tính quảng đường và số lần vật qua vị trí x = -2cm trong khoảng thời gian từ t1 = 0.25s đến t2 = 2.125s, chúng ta cần tìm giá trị của t khi vị trí x bằng -2cm.
Theo phương trình x = 4cos(4πt + x/4), ta có: 4cos(4πt + x/4) = -2 cos(4πt + x/4) = -1/2
Để tìm giá trị của t, ta sử dụng hàm nghịch đảo của hàm cos: 4πt + x/4 = π + 2kπ hoặc 4πt + x/4 = 2π - 2kπ, với k là số nguyên.
Giải phương trình đầu tiên: 4πt + x/4 = π + 2kπ 4πt = π + 2kπ - x/4 t = (π + 2kπ - x/4) / (4π)
Giải phương trình thứ hai: 4πt + x/4 = 2π - 2kπ 4πt = 2π - 2kπ - x/4 t = (2π - 2kπ - x/4) / (4π)
Từ đây, ta có thể tính giá trị của t bằng cách thay x = -2cm, kết hợp với giá trị của k từ t1 đến t2:
t1 = (π + 2kπ + 2/4) / (4π) t2 = (2π - 2kπ + 2/4) / (4π)
Từ đó, ta tính được quảng đường vật đi được: S1 = 4cos(4πt1 + x/4) S2 = 4cos(4πt2 + x/4)
Vậy, quảng đường và số lần vật qua vị trí x = -2cm từ t1=0.25s đến t2=2.125s là S2 - S1 và số lần vật qua vị trí x = -2cm sẽ là số k thỏa mãn trong khoảng từ t1 đến t2

Ta có:
- Chu kì dao động: \(T=\dfrac{2\pi}{\omega}=\dfrac{2\pi}{4\pi}=0,5s\)
\(\Delta t=t_1-t_2=\dfrac{7}{48}s\)
Góc vật quét được khi từ thời điểm \(t_1\) đến \(t_2\) : \(\Delta\varphi=\omega\Delta t=4\pi.\dfrac{7}{48}=105^o\)
Tại thời điểm \(t_1\) vật đang có li độ: \(x=5\left(cm\right)=\dfrac{A}{2}\)
+ Với \(t_1\left(1\right)\) ta có, li độ của vật tại thời điểm \(t_1\left(2\right)\)
\(x_1=A.sin\left(15^o\right)=2,59cm\)
+ Với \(t_2\left(1\right)\) ta có, li độ của vật tại thời điểm \(t_2\left(2\right)\)
\(x_2=A.cos\left(15^o\right)=9,66\left(cm\right)\)\(\Rightarrow A\)
