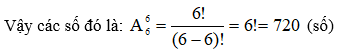Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

f(x1)=3x1f(x1)=3x1
f(x2)=3x2f(x2)=3x2
Theo giả thiết, ta có:
x1<x2⇔3.x1<3.x2x1<x2⇔3.x1<3.x2 ( vì 3>03>0 nên chiều bất đẳng thức không đổi)
⇔f(x1)<f(x2)⇔f(x1)<f(x2) (vì f(x1)=3x1;f(x1)=3x1;f(x2)=3x2)f(x2)=3x2)
Vậy với x1<x2x1<x2 ta được f(x1)<f(x2)f(x1)<f(x2) nên hàm số y=3xy=3x đồng biến trên RR.
Chú ý:
Ta cũng có thể làm như sau:
Vì x1<x2x1<x2 nên x1−x2<0x1−x2<0
Từ đó: f(x1)−f(x2)=3x1−3x2=3(x1−x2)<0f(x1)−f(x2)=3x1−3x2=3(x1−x2)<0
Hay f(x1)<f(x2)f(x1)<f(x2)
Vậy với x1<x2x1<x2 ta được f(x1)<f(x2)f(x1)<f(x2) nên hàm số y=3xy=3x đồng biến trên R
Do \(x_1< x_2\Rightarrow3x_1< 3x_2\)
\(\Rightarrow f\left(x_1\right)< f\left(x_2\right)\)
Hàm số \(f\)đồng biến trên \(ℝ\)khi :
\(\forall x_1,x_2\inℝ\): \(x_1< x_2\Rightarrow f\left(x_1\right)< f\left(x_2\right)\)
=> Hàm số đã cho đồng biến trên \(ℝ\)

em xin lỗi nhưng em chưa đủ tuổi để làm bài này xin cáo từ
xin lỗi quản lý olm ạ
a) Ta có:
f(−2)=23.(−2)=−43;f(−1)=23.(−1)=−23;f(0)=23.0=0;f(12)=23.12=13;f(1)=23.1=23;f(2)=23.2=43;f(3)=23.3=2.f(−2)=23.(−2)=−43;f(−1)=23.(−1)=−23;f(0)=23.0=0;f(12)=23.12=13;f(1)=23.1=23;f(2)=23.2=43;f(3)=23.3=2.
b) Ta có:
g(−2)=23.(−2)+3=53;g(−1)=23.(−1)+3=73;g(0)=23.0+3=3;g(12)=23.12+3=103;g(1)=23.1+3=113;g(2)=23.2+3=133;g(3)=23.3+3=5.g(−2)=23.(−2)+3=53;g(−1)=23.(−1)+3=73;g(0)=23.0+3=3;g(12)=23.12+3=103;g(1)=23.1+3=113;g(2)=23.2+3=133;g(3)=23.3+3=5.
c) Khi biến xx lấy cùng một giá trị thì giá trị của hàm số y=f(x)y=f(x) luôn nhỏ hơn giá trị tương ứng của hàm số y=g(x)y=g(x) là 3 đơn vị.

a, hàm số bậc nhất y = (m-2)x +3 đồng biến <=> m-2 > 0
<=> m >2
b,hàm số bậc nhất y =(m-2)x +3 nghịch biến <=> m - 2 <0
<=> m < 2
a, Để hàm số trên đồng biến khi
\(m-2>0\Leftrightarrow m>2\)
b, Để hàm số trên nghịch biến khi
\(m-2< 0\Leftrightarrow m< 2\)

a: f(x)=3x^2
a=3>0
=>Hàm số đồng biến khi x>0 và nghịch biến khi x<0
b: f(1)=f(-1)=3*1^2=3
f(2)=3*2^2=12
f(-4)=3*(-4)^2=48
c: f(x)=48
=>x^2=48/3=16
=>x=4 hoặc x=-4
d; 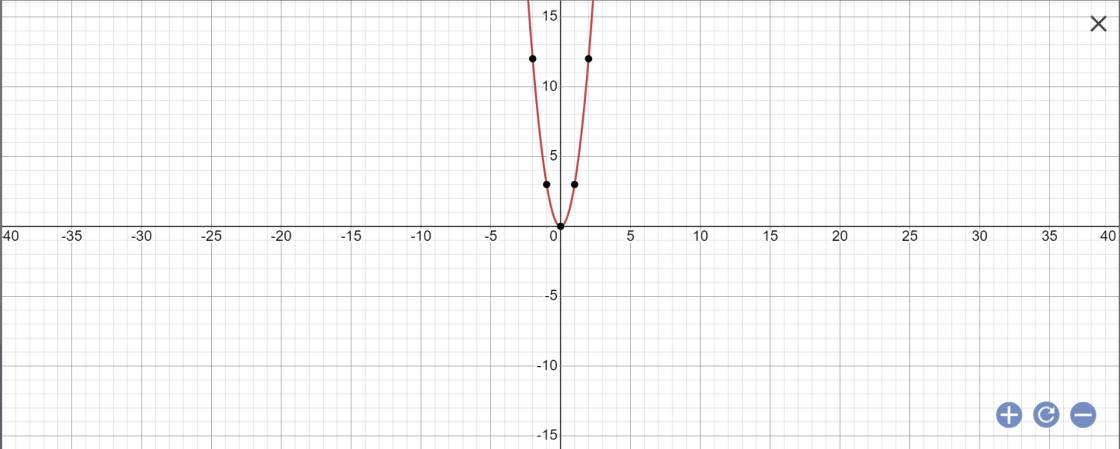

Bài 1:
a) Để lập được số tự nhiên có 6 chữ số khác nhau thì mỗi số như vậy ta coi như một hoán vị của 6 phần tử
P6 = 6! = 720 (số)
b) Số tự nhiên chẵn cần lập có dạng abcdef, với a,b,c,d,e, f là các phần tử khác nhau của các tập hợp {1; 2; 3; 4; 5; 6}, có thứ tự kể đến , f chia hết cho 2.
Để lập được số tự nhiên này, phải thực hiện liên tiếp hai hành động sau đây:
Hành động 1: Chọn chữ số f ở hàng đơn vị, với f chia hết cho 2. Có 3 cách để thực hiện hành động này.
Hành động 2: Chọn một hoán vị của 55 chữ số còn lại (khác với chữ số f đã chọn) để đặt vào các vị trí a,b,c,d,e (theo thứ tự đó). Có 5! cách để thực hiện hành động này.
Theo quy tắc nhân suy ra số các cách để lập được số tự nhiên kể trên là
3.5!=360 (cách)
Qua trên suy ra trong các số tự nhiên có 6 chữ số khác nhau đã lập được từ các chữ số đã cho, có 360 số tự nhiên chẵn.
Tương tự ta tìm được trong các số tự nhiên có 6 chữ số khác nhau đã lập được từ các chữ số đã cho, có 360 số tự nhiên lẻ.
c) Trong các số tự nhiên có 66 chữ số khác nhau lập được từ các chữ số đã cho, những số tự nhiên bé hơn 432000 hoặc là những số tự nhiên có chữ số hàng trăm nghìn nhỏ hơn 4 hoặc là những số tự nhiên có chữ số hàng trăm nghìn là 4 và chữ số hàng chục nghìn nhỏ hơn 3 hoặc là những số tự nhiên có chữ số hàng trăm nghìn là 4 và chữ số hàng chục nghìn là 3 và chữ số hàng nghìn nhỏ hơn 2. Do đó từ các chữ số đã cho, để lập được số tự nhiên có 66 chữ số khác nhau, bé hơn 432000 (ta gọi là số tự nhiên cần lập), phải thực hiện một hành động trong ba hành dộng loại trừ nhau đôi một sau đây:
Hành động 1: Lập số tự nhiên có 6 chữ số khác nhau, với chữ số hàng trăm nghìn nhỏ hơn 4.
Có 3 cách để chọn chữ số hàng trăm nghìn và có 5! cách để chọn một hoán vị của 5 chữ số (đã cho) còn lại, rồi đặt vào các vị trí từ hàng chục nghìn đến hàng đơn vị.
Theo quy tắc nhân suy ra: Số các cách để thực hiện hành động này là:
3.5!=360 (cách).
Hành động 2: Lập số tự nhiên có 6 chữ số khác nhau, với chữ số hàng trăm nghìn là chữ số 4 và chữ số hàng chục nghìn nhỏ hơn 3
Tương tự như trên ta tìm được số các cách để thực hiện hành động này là:
1.2.4!=48 (cách).
Hành động 3: Lập số tự nhiên có 6 chữ số khác nhau, với chữ số hàng trăm nghìn là chữ số 4, chữ số hàng chục nghìn là chữ số 3, chữ số hàng nghìn nhỏ hơn 2
Tương tự như trên ta tìm được số các cách để thực hiện hành động này là:
1.1.1.3!=6 (cách)
Theo quy tắc cộng suy ra số các cách để từ các chữ số khác nhau, lập được từ các chữ số đã cho, có 414 số bé hơn 432000.
Bài 2:
Mỗi cách xếp chỗ ngồi cho 10 người khách vào một dãy 10 ghế là một cách sắp thứ tự cho 10 người khách (theo thứ tự của 10 ghế). Do đó mỗi cách xếp chỗ ngồi là một hoán vị của 10 người khách.
Suy ra số các cách để xếp chỗ ngồi cho 10 người khách vào một dãy 10 ghế là:
P10 = 10! = 3628800 (cách)
Đáp số: 3628800 cách
Bài 3:
Mỗi cách cắm ba bông hoa vào ba lọ là một cách để từ bảy bông hoa, chọn ra ba bông và sắp thứ tự cho chúng (theo thứ tự của ba lọ). Do đó mỗi cách cắm ba bông hoa vào ba lọ là một chỉnh hợp chập 3 của 7 bông hoa. Suy ra số cách cắm hoa là:
A37 = 210 (cách)
Đáp số: 210 cách
mjk giải thế này 0 bt có đúng 0 ,đúng k mjk nha,k đúng nếu mjk lm đúng,ai lp dưới có thể lên mạng xem cx đc nha
Bài 1 (trang 54 SGK Đại số 11): Từ các chữ số 1, 2, 3, 4, 5, 6 lập các số tự nhiên gồm 6 chữ số khác nhau. Hỏi:
a. Có tất cả bao nhiêu số?
b. Có bao nhiêu số chẵn, bao nhiêu số lẻ?
c. Có bao nhiêu số bé hơn 432.000?
Lời giải:
Đặt A = {1, 2, 3, 4, 5, 6 }
a.Tập hợp A gồm 6 phần tử. Để lập được số tự nhiên có 6 chữ số khác nhau thì mỗi số như vậy được coi là một chỉnh hợp chập 6 của 6 phần tử.
b. *Cách 1:
Số chẵn là các số có tận cùng 2, 4, 6
- Gọi số chẵn 6 chữ số khác nhau là abcdef
- Với f = 2, 4, 6 nên có 3 cách chọn f ( f ≠ a, b, c, d, e)
Có 5 cách chọn chữ số a;
Có 4 cách chọn chữ số b (b ≠ a)
Có 3 cách chọn chữ số c(c ≠ a, b);
Có 2 cách chọn chữ số d (d ≠ a, b, c);
Có 1 cách chọn chữ số e (e ≠ a, b, c, d);
Vậy theo quy tắc nhân có: 3.1.2.3.4.5 = 3.5! = 360 (số)
*Cách 2:
Với f = 2, 4, 6 có 3 cách chọn f
a, b, c, d, e ≠ f nên có = 5! cách chọn.
Vậy số cách chọn: 5!.3 = 360 (số)
Gọi số lẻ có 6 chữ số a1b1c1d1e1f1
Ta có: f1 = 1, 3, 5 nên có 3 cách chọn a1, b1, c1, d1, e1 ≠ f1 nên có A 55cách chọn.
Vậy ta có: 3.5! = 360 số
c. Để có một số có 6 chữ số khác nhau lập từ 6 chữ số trên và nhỏ hơn 432.000 ta có thể:
- Chọn chữ số hàng trăm nghìn nhỏ hơn 4: có 3 cách chọn
Với 5 chữ số còn lại có 5! Cách chọn. Số các số như vậy là:
n1 = 3 .5! = 360 số.
- Chọn chữ số đầu là 4, chữ số thứ hai nhỏ hơn 3 và 4 chữ số còn lại.
Số các số như vậy là: n2 = 2.4! = 48 số
- Chọn hai số đầu là 43 và chữ số thứ 3 nhỏ hơn 2:
Số các số như vậy là: n3 = 3! = 6 số
Vậy số các số nhỏ hơn 432.000 là:
n = n1 + n2 + n3= 360 + 48 + 6 = 414 số.

f(x) xác định trên R.
f' (x)=x2+2ax+4;Δf''=a2-4
Cách 1.
+ nếu a2-4<0 hay -2< a < 2 thì f’(x) > 0, ∀x ∈R => hàm số đồng biến trên R.
+ Nếu a2-4=0 hay a=±2
Với a = 2 thì f’(x) = (x+2)2>0 ∀x ≠ -2. Hàm số đồng biến trên R.
Với a = -2 thì f’(x) = (x-2)2>0 ∀x ≠ 2. Hàm số đồng biến trên R.
+ Nếu a2-4>0 hay a< - 2 hoặc a> 2 thì f’(x) = 0 có 2 nghiệm phân biệt x1,x2. Giả sử x1<x2, khi đó hàm số nghịch biến trên khoảng (x1,x2). Vậy các giá trị này của a không thõa mãn yên cầu bài toán.
Cách 2.
Hàm số đồng biến trên R khi và chỉ khi f’(x) > 0 ∀x ∈R f’(x) = 0 chỉ tại một số hữu hạn điểm.
Kết luận: hàm số đồng biến trên R khi và chỉ khi -2≤ a≤2

Theo đề, ta có hệ phương trình:
\(\left\{{}\begin{matrix}a+b=2\\-a+b=\sqrt{2}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2b=2+\sqrt{2}\\a+b=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}b=\sqrt{2}+1\\a=1-\sqrt{2}\end{matrix}\right.\)
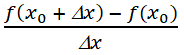 khi Δx → 0 trong hai trường hợp Δx > 0 và Δx < 0.
khi Δx → 0 trong hai trường hợp Δx > 0 và Δx < 0.