S
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
13 tháng 4 2020
Bài 1. B = 1 + 2 + 3 + ... + 98 + 99
Số số hạng : ( 99 - 1 ) : 1 + 1 = 99 số
Tổng : ( 99 + 1 ) . 99 : 2 = 4950
=> B = 4950
Công thức
Tính số số hạng : ( số lớn - số bé ) : khoảng cách + 1
Tính tổng : ( số lớn + số bé ) . số số hạng : 2
=> Tương tự với C và D
13 tháng 4 2020
Bài 1:
Dãy B có số số hạng là:(99-1):1 +1=99 số số hạng
=> B=\(\frac{\left(99+1\right)\cdot99}{2}=4950\)
Bài 2:
Dãy C có số số hạng là: (999-1):2+1=500 số số hạng
=> \(C=\frac{\left(999+1\right)\cdot500}{2}=250000\)
Bài 3: làm tương tự
D
8
5 tháng 4 2018
số số hạng là: (99-1):1 +1 = 99(số)
tổng của dãy số đó là: (99+1) x99 :2=4950
k mk^_^
K
2
NY
15 tháng 9 2019
Bài 1:
B = 1 + (2 + 3 + 4 + ... + 98 + 99).
Ta thấy tổng trong ngoặc gồm 98 số hạng, nếu chia thành các cặp ta có 49 cặp nên tổng đó là:
(2 + 99) + (3 + 98) + ... + (51 + 50) = 49.101 = 4949
Khi đó B = 1 + 4949 = 4950
Bài 2:
3A = 1.2.3 + 2.3.3 + … + n(n + 1).3 = 1.2.(3 - 0) + 2.3.(3 - 1) + … + n(n + 1)[(n - 2) - (n - 1)] = 1.2.3 - 1.2.0 + 2.3.3 - 1.2.3 + … + n(n + 1)(n + 2) - (n - 1)n(n + 1) = n(n + 1)(n + 2) 
* Tổng quát hoá ta có:
k(k + 1)(k + 2) - (k - 1)k(k + 1) = 3k(k + 1). Trong đó k = 1; 2; 3; …
Ta dễ dàng chứng minh công thức trên như sau:
k(k + 1)(k + 2) - (k - 1)k(k + 1) = k(k + 1)[(k + 2) - (k - 1)] = 3k(k + 1)
#Châu's ngốc
NY
15 tháng 9 2019
lm lại bài 2:
3A = 1.2.3 + 2.3.3 + … + n(n + 1).3 = 1.2.(3 - 0) + 2.3.(3 - 1) + … + n(n + 1)[(n - 2) - (n - 1)] = 1.2.3 - 1.2.0 + 2.3.3 - 1.2.3 + … + n(n + 1)(n + 2) - (n - 1)n(n + 1) = n(n + 1)(n + 2)
=>A=\(\frac{n\times\left(n+1\right)\left(n+2\right)}{3}\)
* Tổng quát hoá ta có:
k(k + 1)(k + 2) - (k - 1)k(k + 1) = 3k(k + 1). Trong đó k = 1; 2; 3; …
Ta dễ dàng chứng minh công thức trên như sau:
k(k + 1)(k + 2) - (k - 1)k(k + 1) = k(k + 1)[(k + 2) - (k - 1)] = 3k(k + 1)
2 tháng 5 2018
:v cả chuyên mục câu hỏi hay :V
Câu 1:
Số số hạng của dãy là:
(99-1):1+1=99( số hạng)
Tổng của dãy trên là:
(99+1).99:2=4950
Câu 2:
Số hạng của dãy là:
(999-1):2+1=500 ( số hạng)
Tổng của dãy trên là:
(999+1).500:2=250000
Câu 3:
Số hạng của dãy là:
(998-10):2+1=495 ( số hạng)
Tổng của dãy trên là:
(998+10).495:2=249480
2 tháng 5 2018
Bài 1
Số số hạng = ( 99 - 1 ) : 2 + 1 = 99
B = ( 1 + 99 ) x 99 : 2 = 4950
Bài 2
Số số hạng = ( 999 - 1 ) : 2 + 1 = 500
C = ( 1 + 999 ) x 500 : 2 = 250000
Bài 3
Số số hạng = ( 998 - 10 ) : 2 + 1 = 495
D = ( 10 + 998 ) x 495 : 2 = 249480
MT
2
25 tháng 12 2020
Tính B = 1 + 2 + 3 + ... + 98 + 99
Tổng B có SSH là : ( 99 - 1 ) : 1 + 1 = 99
Tổng B là : ( 99 + 1 ) x 99 : 2 = 4950
Vậy Tổng B = 4950
25 tháng 12 2020
B= 1 + 2 + 3 +.......+98 + 99
B có số số hạng là :
( 99 - 1 ) : 1 + 1 =99 ( số)
Tổng của biểu thức trên là ( B là )
(99 + 1) x 99 : 2 =4950
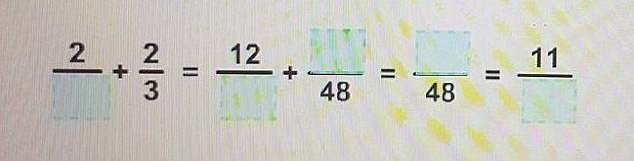
1 Giải
Số lượng số hạng là:
(99-1):1+1=99(số hạng)
Tổng dãy B là:
(99+1).99:2=4950
Đ/S:4950