Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có:\(\left(x-y\right)\left(x^2+xy+y^2\right)=x^3-y^3\)
với \(x=-10;y=2\) ,ta có:
\(\left(-10\right)^3-2^3=-1000-8=-1008\)
với \(x=-1;y=0\)
\(\left(-1\right)^3-0^3=-1-0=-1\)
với \(x=2;y=-1\) ,ta có:
\(2^3-\left(-1\right)^3=8-\left(-1\right)=8+1=9\)
với \(x=-0,5;y=1,25\), ta có:
\(\left(-0,5\right)^3-1,25^3=0-2=-2\)
Ta có bảng sau;
| Giá trị của x và y |
Giá trị của biểu thức \(\left(x-y\right)\left(x^2+xy+y^2\right)\) |
| \(x=-10;y=2\) | \(\left(x-y\right)\left(x^2+xy+y^2\right)=-1008\) |
| \(x=-1;y=0\) | \(\left(x-y\right)\left(x^2+xy+y^2\right)=-1\) |
| \(x=2;y=-1\) | \(\left(x-y\right)\left(x^2+xy+y^2\right)=9\) |
| \(x=-0,5;y=1,25\) | \(\left(x-y\right)\left(x^2+xy+y^2\right)=-2\) |
Trước hết, ta làm tính nhân để rút gọn biểu thức, ta được:
(x - y)(x2 + xy + y2) = x . x2 + x . xy + x . y2 + (-y) . x2 + (-y) . xy + (-y) . y2
= x3 + x2y + xy2 – yx2 – xy2 – y3 = x3 – y3
Sau đó tính giá trị của biểu thức x3 – y3
Ta có:
Khi x = -10; y = 2 thì A = (-10)3 – 23 = -1000 – 8 = 1008
Khi x = -1; y = 0 thì A = (-1)3 – 03 = -1
Khi x = 2; y = -1 thì A = 23 – (-1)3 = 8 + 1 = 9
Khi x = -0,5; y = 1,15 thì
A = (-0,5)3 – 1,253 = -0,125 – 1.953125 = -2,078125

Ta có:
N: x3 – 3x2 + 3x – 1 = x3 – 3 . x2. 1+ 3 . x .12 – 13 = (x – 1)3
U: 16 + 8x + x2= 42 + 2 . 4 . x + x2 = (4 + x)2
= (x + 4)2
H: 3x2 + 3x + 1 + x3 = x3 + 3x2 + 3x + 1
= (x + 1)3 = (1 + x)3
Â: 1 – 2y + y2 = 12 - 2 . 1 . y + y2 = (1 - y)2
= (y - 1)2
Nên:
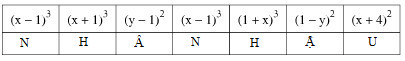
Vậy: Đức tính đáng quý là "NHÂN HẬU"
Chú ý:
Có thế khai triển các biểu thức (x – 1)3 , (x + 1)3 , (y - 1)2 , (x + 4)2 ... để tìm xem kết quả ứng với chữ nào và điền vào bảng.
Bài giải:
Ta có:
N: x3 – 3x2 + 3x – 1 = x3 – 3 . x2. 1+ 3 . x .12 – 13 = (x – 1)3
U: 16 + 8x + x2= 42 + 2 . 4 . x + x2 = (4 + x)2
= (x + 4)2
H: 3x2 + 3x + 1 + x3 = x3 + 3x2 + 3x + 1
= (x + 1)3 = (1 + x)3
Â: 1 – 2y + y2 = 12 - 2 . 1 . y + y2 = (1 - y)2
= (y - 1)2
Nên:
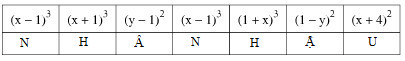
Vậy: Đức tính đáng quý là "NHÂN HẬU"
Chú ý:
Có thế khai triển các biểu thức (x – 1)3 , (x + 1)3 , (y - 1)2 , (x + 4)2 ... để tìm xem kết quả ứng với chữ nào và điền vào bảng.

a) Ta có :
\(5x-3=x^2-3x+12\left(1\right)\)
\(x^2-3x+12=\left(x+1\right)\left(x-3\right)\left(2\right)\)
\(\left(x+1\right)\left(x-3\right)=5x-3\left(3\right)\)
b) Lập bảng :
| x | -5 | -4 | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 | 5 |
| 5x - 3 | -28 | -23 | -18 | -13 | -8 | -3 | 2 | 7 | 12 | 17 | 22 |
| \(x^2-3x+12\) | 52 | 40 | 30 | 22 | 16 | 12 | 10 | 10 | 12 | 16 | 22 |
| (x+1)(x-3) | 32 | 21 | 12 | 5 | 0 | -3 | -4 | -3 | 0 | 5 | 12 |
Từ bảng trên , ta có :
- Phương trình (1) có có tập nghiệm là \(S=\left\{3;5\right\}\)
- Phương trình (2) vô nghiệm \(S=\varnothing\)
- Phương trình (3) có tập nghiệm là \(S=\left\{0\right\}\)

Gọi x(cm) là độ dài cạnh của hlp ( x > 0 )
Theo định lí Pythagoras ta có : \(2x^2=25\Leftrightarrow x=\frac{5\sqrt{2}}{2}\left(cm\right)\)vì x > 0
\(\Rightarrow S_{tp}=\left(\frac{5\sqrt{2}}{2}\right)^2\cdot6=75cm^2\)

Thay x = -1, y = 1 vào biểu thức, ta được
a(-1)(-1 - 1) + 13(-1 + 1) = -a(-2) + 10 = 2a.
Vậy đánh dấu x vào ô trống tương ứng với 2a.
2: \(8xy-24xy+16x\)
\(=8x\cdot y-8x\cdot3y+8x\cdot2\)
\(=8x\left(y-3y+2\right)=8x\left(-2y+2\right)\)
\(=-16y\left(y-1\right)\)
3: \(xy-x=x\cdot y-x\cdot1=x\left(y-1\right)\)
11: \(2mx-4m2xy+6mx\)
\(=2mx-2my\cdot4y+2mx\cdot3\)
\(=2mx\left(1-4y+3\right)\)
\(=2mx\left(4-4y\right)=8mx\left(1-y\right)\)
12: \(7x^2y^5-14x^3y^4-21y^3\)
\(=7y^3\cdot x^2y^2-7y^3\cdot2x^3y-7y^3\cdot3\)
\(=7y^3\left(x^2y^2-2x^3y-3\right)\)
13: \(2\left(x-y\right)-a\left(x-y\right)\)
\(=2\cdot\left(x-y\right)-a\cdot\left(x-y\right)\)
\(=\left(x-y\right)\left(2-a\right)\)