Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi khối lượng hàng mỗi ngày phải chở theo kế hoạch là x
=>Thời gian hoàn thành là 140/x
Theo đề, ta có: \(\dfrac{140}{x}-\dfrac{150}{x+5}=1\)
=>\(140x+700-150x=\left(x^2+5x\right)\)
=>x^2+5x=-10x+700
=>x^2+15x-700=0
=>(x+35)(x-20)=0
=>x=20
gọi tgian đội xe chở hết hàng là x(ngày) (x>1)
thời gian thực tế là: x-1 (ngày)
mỗi ngày theo kế hoạch đội xe đó chở: \(\dfrac{140}{x}\) (tấn)
thực tế chở được 140+10=150 (tấn)
=> mỗi ngày chở được: \(\dfrac{150}{x-1}\) (tấn)
theo đb, mỗi ngày đội đó chở vượt mức 5 tấn, nên ta có pt:
\(\dfrac{150}{x-1}\) - \(\dfrac{140}{x}\) =5 (tu giai)
<=> x=7(tm) (x=-4 => loại)
vật tgian đội đó chở hết hàng theo kh là 7 ngày

Giải
Gọi khối lượng hàng chở theo định mức trong 1 ngày của đội là x ( tấn ) ( x > 0)
Số ngày quy định là \(\frac{140}{x}\)( ngày )
Do vượt mức nên số ngày đội đã chở là \(\frac{140}{x}\)= \(1\)( ngày)
Khối lượng hàng đội đã chở được là \(140\)+\(10\)= \(150\) ( tấn )
Theo đề bài ta có phương trình:
<=> ( \(\frac{140}{x}\)- \(1\)) ( \(x\)+ \(5\)) = \(140\)+ \(10\)
<=> (\(140\)- \(x\)) ( \(x\)+ \(5\)) = \(150x\)
<=> \(140x\)+ \(700\)- \(5x\)- X2
<=> X2 + \(15x\)- \(700\)= \(0\)
Giải ra \(x\)= \(20\)( T/M) và \(x\)= - \(35\)( loại )
Vậy số ngày đội phải chở theo kế hoạch là : \(140\): \(20\)= \(7\)( ngày )
Đáp số : \(7\)ngày.

Gọi thời gian đội chở hàng và số hàng đội cần chở mỗi ngày theo kế hoạch lần lượt là x (ngày) và y (tấn/ngày)
ĐK: x ∈ N*; x > 1
Theo đề bài ta có hệ phương trình x y = 200 x - 1 y + 4 = 216
Giải ra ta được x = 10; y = 20 (TMĐK)
Kết luận

Gọi số sản phẩm đội dự định làm mỗi ngày là x (x ∈ ℕ * , x < 84) (sản phẩm)
*) Theo kế hoạch, thời gian hoàn thành là 1000/x (ngày)
*) Thực tế, mỗi ngày làm được x + 10 (sản phẩm)
Thời gian hoàn thành 1000/(x+10) (ngày)
Vì thời gian thực tế ít hơn thời gian dự định là 2 ngày nên ta có phương trình:
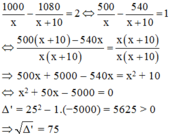
Phương trình có hai nghiệm phân biệt: x 1 = − 25 – 75 = −100 (loại)
và x 2 = −25 + 75 = 50 (tmđk)
Vậy theo kế hoạch, mỗi ngày tổ dự định làm 50 sản phẩm
Đáp án: C

Gọi x là sản ppham xưởng sản xuất trong 1 ngày theo kế hoạch (x>0)
=>Số ngày theo kế hoạch là :\(\frac{110}{x}\)
Số ngày thực tế là \(\frac{1100}{x+5}\)theo gia thiet cua bai toan ta co :
\(\frac{1100}{x}-\frac{1100}{x+5}=2\)
<=>1100(x+5)-1100x=2x(x+5)
<=>2x^2+10x-5500=0
<=>x=50hay x=-55 loai
Vậy theo kế hoạch mỗi ngày phân xưởng phải sản xuất là 50 sản phẩm
Gọi số sản phẩm mà phân xưởng làm trong 1 ngày là x ( x > 0 )
=> Số ngày quy định = \(\frac{1100}{x}\)( ngày )
Mỗi ngày phân xưởng sản xuất vượt mức 5 sản phẩm
=> Số ngày hoàn thành = \(\frac{1100}{x+5}\)( ngày )
Vì thế kế hoạch hoàn thành sớm hơn quy định 2 ngày
=> Ta có phương trình : \(\frac{1100}{x}-\frac{1100}{x+5}=2\)
\(\Leftrightarrow\frac{1100\left(x+5\right)}{x\left(x+5\right)}-\frac{1100\cdot x}{x\left(x+5\right)}=\frac{2x\left(x+5\right)}{x\left(x+5\right)}\)
\(\Leftrightarrow1100x+5500-1100x=2x^2+10x\)
\(\Leftrightarrow2x^2+10x-1100x-5500+1100x=0\)
\(\Leftrightarrow2x^2+10x-5500=0\)
\(\Delta'=b'^2-ac=5^2-2\cdot\left(-5500\right)=25+11000=11025\)
\(\Delta'>0\)nên phương trình đã cho có hai nghiệm phân biệt :
\(\hept{\begin{cases}x_1=\frac{-b'+\sqrt{\Delta'}}{a}=\frac{-5+\sqrt{11025}}{2}=50\\x_2=\frac{-b-\sqrt{\Delta'}}{a}=\frac{-5-\sqrt{11025}}{2}=-55\end{cases}}\)
x > 0 => x = 50
Vậy theo kế hoạch , mỗi ngày phân xưởng sản xuất 50 sản phẩm
Bài 1 :
Gọi số người của đội là \(x\) người \(\left(x\inℕ^∗\right)\)
Thời gian làm theo kế hoạch là \(\frac{420}{x}\) ngày
Số người lúc sau là \(x+5\) người
Thời gian hoàn thành lúc sau là \(\frac{420}{x+5}\) ngày
Vì thời gian giảm 7 ngày nên ta có phương trình :
\(\frac{420}{x}-7=\frac{420}{x+5}\)
\(\Leftrightarrow420\left(x+5\right)-7x\left(x+5\right)=420x\)
\(\Leftrightarrow420x+2100-7x^2-35x-420x\)
\(\Leftrightarrow7x^2+35x-2100=0\)
\(\Leftrightarrow x^2+5x-300=0\)
\(\Leftrightarrow\left(x+20\right)\left(x-15\right)=0\)
\(\Leftrightarrow x=15\) \(\left(x\inℕ^∗\right)\)
Vậy số người của đội là 15 người.