Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

2:
a: Xét ΔOAB có OA=OB=AB
nên ΔOAB đều
=>\(\widehat{AOB}=60^0\)
=>Số đo cung nhỏ AB là 600
Số đo cung lớn AB là 360-60=3000
b: ΔOAB đều
mà OI là đường trung tuyến
nên \(OI=AB\cdot\dfrac{\sqrt{3}}{2}=\dfrac{R\sqrt{3}}{2}\)
c: Xét (O) có
MA,MB là tiếp tuyến
=>MA=MB
=>M nằm trên đường trung trực của AB(1)
ΔOAB cân tại O
mà OI là đường trung tuyến
nên OI là đường trung trực của AB(2)
Từ (1),(2) suy ra O,I,M thẳng hàng

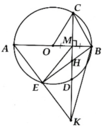
a, Chứng minh được ∆COD đều => A M B ^ = 60 0
b, A B C ^ = 30 0 => A O C ^ = 60 0 => l A C ⏜ = πR 3

giải b2:
a, MPHQ là hình chữ nhật => MH = PQ
b, Sử dụng hệ thức lượng trong tam giác vuông chứng minh được MP.MA = MQ.MB => ∆MPQ: ∆MBA
c,\(\widehat{PMH}=\widehat{MBH}\Rightarrow\widehat{PQH}=\widehat{O_2QP}\) => PQ là tiếp tuyến của \(\left(O_2\right)\)
Tương tự PQ cũng là tiếp tuyến \(\left(O_1\right)\)

* Số đo cung nhỏ AB=góc AOB( góc ở tâm)\(\Rightarrow\) Số đo cung nhỏ AB=60 độ
* Diện ích hình quạt tròn OAB là
\(S=\frac{\pi\times R2\times n}{360}=\frac{\pi\times9\times60}{360}=\frac{3}{2}\pi\approx\frac{3}{2}\times3,14\approx4,71\)cm2
* Số đo cung lớn AB= 360 độ - 60 độ =300 độ
Độ dài cung lớn AB là:
l=3,14*3*300/180=15,7 cm


Câu 3:
a: Độ dài cung nhỏ AB là:
\(\dfrac{2\cdot pi\cdot R\cdot120}{360}=\dfrac{pi\cdot R\cdot2}{3}\)
Độ dài cung nhỏ BC là;
\(\dfrac{2\cdot pi\cdot R\cdot120}{360}=pi\cdot R\cdot\dfrac{2}{3}\)
b: \(S=\dfrac{pi\cdot R^2\cdot120}{360}=pi\cdot R^2\cdot\dfrac{1}{3}\)
c: Diện tích hình quạt tròn OAC là:
\(S_q=\dfrac{pi\cdot R^2\cdot120}{360}=pi\cdot\dfrac{R^2}{3}\)
Diện tích tam giác OAC là:
\(S=\dfrac{1}{2}\cdot OA\cdot OC\cdot sin120=\dfrac{1}{4}\cdot R^2\)
Diện tích hình viên phân OAC là;
\(S_q-S=R^2\left(\dfrac{pi}{3}-\dfrac{1}{4}\right)\)