Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
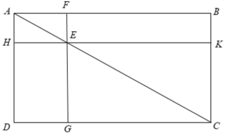
Theo giả thiết ta có FG//AD, HK//AB nên HE//AF và AH//EF.
Xét tứ giác AFEH có:
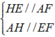⇒ AFEH là hình bình hành.
Đề sai rồi, em kiểm tra lại, EK, HF và BD ko hề đồng quy
Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB < MD. Đường thẳng qua M và song song với AB cắt AD và BC lần lượt tại E và F. Đường thẳng qua M song song với AD cắt AB và AC lần lượt tại K và H.
1. Chứng minh: các đường thẳng EK, HF, BD đồng quy
2. Cho SMKF = 9 cm2 ; SMEH = 25 cm2 . Tính SABCD.
AE = CF (gt)
mà AE // CF (ABCD là hình chữ nhật)
=> AECF là hình bình hành
=> FA // CE
=> AFD = ECF (2 góc đồng vị)
mà ECF = CEB (2 góc so le trong, AB // CD)
=> AFD = CEB (1)
AB = CD (ABCD là hình chữ nhật)
mà AE = CF (gt)
=> AB - AE = CD - CF
=> EB = DF (2)
Xét tam giác NEB và tam giác MFD có:
NEB = MFD (theo 1)
EB = FD (theo 2)
EBN = FDM (2 góc so le trong, AB // CD)
=> Tam giác NEB = Tam giác MFD (g.c.g)
=> BN = DM (2 cạnh tương ứng)
O là trung điểm của BD (3)
=> O là trung điểm của AC (ACBD là hình chữ nhật) (4)
=> O là trung điểm của EF (AECF là hình bình hành) (5)
AEI = ABD (2 góc so le trong, EI // BD)
CFK = CDB (2 góc so le trong, FK // BD)
mà ABD = CBD (2 góc so le trong, AB // CD)
=> AEI = CFK (6)
EI // BD (gt)
FK // DB (gt)
=> EI // FK (7)
Xét tam giác EAI và tam giác FCK có:
IEA = KFC (theo 6)
EA = FC (gt)
EAI = FCK (= 900)
=> Tam giác EAI = Tam giác FCK (g.c.g)
=> EI = FK (2 cạnh tương ứng)
mà EI // FK (theo 7)
=> EIFK là hình bình hành
mà O là trung điểm của EF (theo 5)
=> O là trung điểm của IK (8)
Từ (3), (4), (5) và (8)
=> AC, EF, IK đồng quy tại O là trung điểm của BD
O là trung điểm của AC và BD
=> OA = OC = \(\frac{AC}{2}\)
OB = OD = \(\frac{BD}{2}\)
mà AC = BD (ABCD là hình chữ nhật)
=> OA = OD = OB = OC
=> Tam giác OAD cân tại O
mà AOD = 600
=> Tam giác OAD đều
=> AD = OA = OD
mà AD = 1 cm
AD = BC (ABCD là hình chữ nhật)
=> OA = OD = OC = OB = BC = 1 cm
=> AC = 2OA = 2 . 1 = 2 cm
Xét tam giác BAC vuông tại B có:
\(AC^2=BA^2+BC^2\) (định lý Pytago)
\(AB^2=AC^2-BC^2\)
\(=2^2-1^2\)
\(=4-1\)
= 3
\(AB=\sqrt{3}\)
\(S_{ABCD}=AB\times BC=\sqrt{3}\times1=\sqrt{3}\left(cm^2\right)\)
Answer:
a) Gọi I và J là giao điểm các đường chéo của hình chữ nhật MDNF và hình chữ nhật ABCD
Tam giác IND và tam giác JCD là các tam giác cân \(\Rightarrow\widehat{N_1}=\widehat{D_1}\) và \(\widehat{C_1}=\widehat{D_2}\)
Mặt khác \(\widehat{N_1}=\widehat{D_2}\) (Hai góc đồng vị)
Vậy \(\widehat{C_1}=\widehat{D_1}\Rightarrow DF//AC\)
b) Tứ giác EIDJ là hình bình hành vì có các cạnh đối song song
Có: EJ = ID nhưng IF = ID \(\Rightarrow IF=EJ\)
Từ đó tứ giác EFIJ là hình bình hành \(\Rightarrow FE=IJ\left(1\right)\)
Mặt khác trong tam giác FBD: có FB // IJ (2)
Từ (1) và (2) => điểm E, điểm B, điểm F thẳng hàng
Mà EF = IJ và EB = IJ
=> E là trung điểm BF
Gọi H là trung điểm DC.
Chứng minh HE// IF( vì cùng //BC)
=> HE vuông FK ( vì FK vuông IF)
Tương tự HF// EI( vì cùng //AD)
=> HF vuông EK( vì EK vuông IE)
Xét tam giác EFH có EK và FK là 2 đường cao nên K là trực tâm. Suy ra HK vuông FE mà FE //DC nên HK vuông DC tại H suy ra tam giác KDC cân tại K. Nên KD=KC
a) F H A ^ = H A K ^ = A K F ^ = 90 0
Þ AHFK là hình chữ nhật.
b) Gọi là giao điểm của AC và BD. Chứng minh OE là đường trung bình của DACF
Þ AF//OE
Þ AF/BD
c) Gọi I là giao điểm của AF và HK.
Chứng minh
H 1 ^ = A ^ 1 ( H 1 ^ = A 2 ^ = B 1 ^ = A 1 ^ ) ⇒ K H / / A C mà KH đi qua trung điểm I của AF Þ KH đi qua trung điểm của FC.
Mà E là trung điểm của FC Þ K, H, E thẳng hàng
