Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Quan sát đồ thị:
điểm \(\left( {1; - 2} \right)\) (tức là có x =1; y=-2) thuộc đồ thị.
điểm \(\left( {2; - 1} \right)\) (tức là có x=2; y=-1) thuộc đồ thị hàm số.
điểm (0;0) không thuộc đồ thị hàm số.
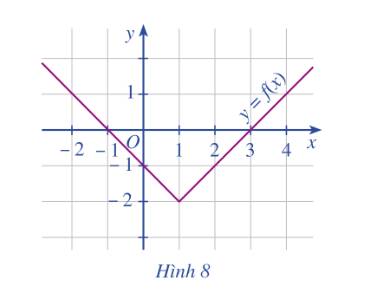
b) Từ điểm trên Ox: \(x = 0\) ta kẻ đường thẳng song song với Oy ta được: \(f\left( 0 \right) = - 1\)
Từ điểm trên Ox: \(x = 3\) ta kẻ đường thẳng song song với Oy ta được: \(f\left( 3 \right) = 0\)
c) Giao điểm của đồ thị và trục Ox là điểm \(\left( {3;0} \right)\).

Bài 1:
\(f\left(-x\right)=\left|\left(-x\right)^3+x\right|=\left|-x^3+x\right|=\left|-\left(x^3-x\right)\right|=\left|x^3-x\right|=f\left(x\right)\)
Vậy hàm số chẵn
Bài 2:
\(f\left(4\right)=4-3=1\\ f\left(-1\right)=2.1+1-3=0\\ b,\text{Thay }x=4;y=1\Leftrightarrow4-3=1\left(\text{đúng}\right)\\ \Leftrightarrow A\left(4;1\right)\in\left(C\right)\\ \text{Thay }x=-1;y=-4\Leftrightarrow2\left(-1\right)^2+1-3=-4\left(\text{vô lí}\right)\\ \Leftrightarrow B\left(-1;-4\right)\notin\left(C\right)\)

a: TXĐ: D=R
b: \(f\left(-1\right)=\dfrac{2}{-1-1}=\dfrac{2}{-2}=-1\)
\(f\left(0\right)=\sqrt{0+1}=1\)
\(f\left(1\right)=\sqrt{1+1}=\sqrt{2}\)
\(f\left(2\right)=\sqrt{3}\)

a) Hệ số a là: a=1
\(f(0) = {0^2} - 4.0 + 3 = 3\)
\(f(1) = {1^2} - 4.1 + 3 = 0\)
\(f(2) = {2^2} - 4.2 + 3 = - 1\)
\(f(3) = {3^2} - 4.3 + 3 = 0\)
\(f(4) = {4^2} - 4.4 + 3 = 3\)
=> f(0); f(4) cùng dấu với hệ số a; f(2) khác dấu với hệ số a
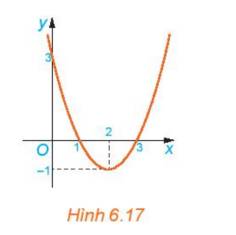
b) Nhìn vào đồ thị ta thấy
- Trên khoảng \(\left( { - \infty ;1} \right)\) đồ thị nằm phía trên trục hoành
- Trên khoảng \(\left( {1;3} \right)\), đồ thị nằm phía dưới trục hoành
- Trên khoảng \(\left( {3; + \infty } \right)\), đồ thị nằm phía trên trục hoành
c) - Trên khoảng \(\left( { - \infty ;1} \right)\) đồ thị nằm phía trên trục hoành => f(x)>0, cùng dầu với hệ số a
- Trên khoảng \(\left( {1;3} \right)\), đồ thị nằm phía dưới trục hoành => f(x) <0, khác dấu với hệ số a
- Trên khoảng \(\left( {3; + \infty } \right)\), đồ thị nằm phía trên trục hoành => f(x)>0, cùng dấu với hệ số a

a: \(f\left(-2\right)=\left(-2\right)^2+3\cdot\left(-2\right)-1\)
=4-6-1
=-3
\(f\left(-1\right)=\left(-1\right)^2+3\cdot\left(-1\right)-1\)
\(=1-3-1\)
=-3

a: TXĐ: \(D=R\backslash\left\{-\dfrac{1}{2}\right\}\)
b: TXĐ: \(D=R\backslash\left\{-3;1\right\}\)
c: TXĐ: \(D=\left[-\dfrac{1}{2};3\right]\)

a.
\(\Leftrightarrow x^2+2\left(m-1\right)x+m^2+3m+5\ne0\) ; \(\forall x\)
\(\Leftrightarrow\Delta'=\left(m-1\right)^2-\left(m^2+3m+5\right)< 0\)
\(\Leftrightarrow-5m-4< 0\)
\(\Leftrightarrow m>-\dfrac{4}{5}\)
b.
\(\Leftrightarrow x^2+2\left(m-1\right)x+m^2+m-6\ge0\) ;\(\forall x\)
\(\Leftrightarrow\Delta'=\left(m-1\right)^2-\left(m^2+m-6\right)\le0\)
\(\Leftrightarrow-3m+7\le0\)
\(\Rightarrow m\ge\dfrac{7}{3}\)
c.
\(x^2-2\left(m+3\right)x+m+9>0\) ;\(\forall x\)
\(\Leftrightarrow\Delta'=\left(m+3\right)^2-\left(m+9\right)< 0\)
\(\Leftrightarrow m^2+5m< 0\Rightarrow-5< m< 0\)

a) f(-\(\dfrac{1}{2}\))= - \(\dfrac{1}{2}\)+1=\(\dfrac{1}{2}\)
f(0)=0+1=1
f(-1)=-1+1=0
b) f(x)=0 <=> x+1=0 <=>x=-1
f(x)=2 <=> x+1=2 <=>x=1
c) với điểm A(\(\dfrac{3}{4}\);\(\dfrac{-1}{2}\)) thay vào hàm số ta có -2*\(\dfrac{3}{4}\)+1=\(\dfrac{-1}{2}\)=\(\dfrac{-1}{2}\)
=> điểm A có thuộc đồ thị hàm số trên
làm tương tự vs các điểm còn lại nha bạn !