Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài 2:
\(x^2-2x-3-\left(x+1\right)\sqrt{x^2+3}=0\)
\(\Leftrightarrow\left(x+1\right)\left(x-3\right)-\left(x+1\right)\sqrt{x^2+3}=0\)
\(\Leftrightarrow\left(x+1\right)\left(x-3-\sqrt{x^2+3}\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}x+1=0\\x-3-\sqrt{x^2+3}=0\end{cases}}\)
TH1: \(x+1=0\Leftrightarrow x=-1\)
TH2: \(x-3-\sqrt{x^2+3}=0\Leftrightarrow x-3=\sqrt{x^2+3}\)
\(\Leftrightarrow\hept{\begin{cases}x\ge3\\x^2+3=x^2-6x+9\end{cases}}\Leftrightarrow\hept{\begin{cases}x\ge3\\x=1\end{cases}}\left(l\right)\)
Vậy phương trình có nghiệm x = -1.

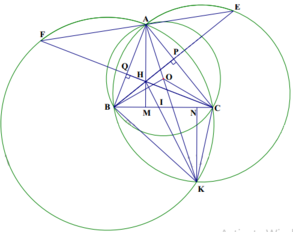
Gọi (O’) là đường tròn đi qua bốn điểm B, H,C, K. Ta có dây cung B C = R 3
BKC=60o= BAC nên bán kính đường tròn (O’) bằng bán kính R của đường tròn (O).
Gọi M là giao điểm của AH và BC thì MH vuông góc với BC, kẻ KN vuông góc với BC (N thuộc BC), gọi I là giao điểm của HK và BC.

a) Ta có : \(\widehat{MOA}=\widehat{O_1}'\left(=180^o-2\widehat{A_1}\right)\)
\(\Rightarrow\)O'N // OM
Gọi P là giao điểm của MN và OO'
Ta có : \(\frac{O'P}{OP}=\frac{O'N}{OM}=\frac{R'}{R}\)
gọi P' là giao điểm của BC và OO',ta có :
\(\frac{O'P'}{OP'}=\frac{O'C}{OB}=\frac{R'}{R}\)
Suy ra \(P'\equiv P\)
b) gọi H là hình chiếu của O' trên OM
tứ giác MNO'O là hình thang nên \(S=\frac{\left(OM+O'N\right)O'H}{2}\)
\(S=\frac{R+R'}{2}.O'H\le\frac{R+R'}{2}.OO'=\frac{\left(R+R'\right)^2}{2}\)
Dấu "=" xảy ra khi \(H\equiv O\Leftrightarrow OM\perp OO'\)
Vậy ...
2/ Đặt \(\sqrt{x^2+3}=a\ge0\) thì ta có
\(a^2-2x-6-\left(x+1\right)a=0\)
\(\Leftrightarrow\left(a+2\right)\left(a-x-3\right)=0\)
\(\Leftrightarrow a=x+3\)
\(\Leftrightarrow\sqrt{x^2+3}=x+3\)
Làm nốt nhé