Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét (O) có
MA là tiếp tuyến có A là tiếp điểm
MB là tiếp tuyến có B là tiếp điểm
Do đó: MA=MB
Xét ΔMAB có MA=MB
nên ΔMAB cân tại M
Suy ra: \(\widehat{MAB}=\widehat{MBA}\)
Xét ΔDAB vuông tại D và ΔEBA vuông tại E có
BA chung
\(\widehat{DBA}=\widehat{EAB}\)
Do đó: ΔDAB=ΔEBA
Suy ra: \(\widehat{DAB}=\widehat{EBA}\)
hay \(\widehat{HAB}=\widehat{HBA}\)
Xét ΔHBA có \(\widehat{HAB}=\widehat{HBA}\)
nên ΔHBA cân tại H
Suy ra: HA=HB
hay H nằm trên đường trung trực của AB(1)
Ta có:MA=MB
nên M nằm trên đường trung trực của AB(2)
Ta có: OA=OB
nên O nằm trên đường trung trực của AB(3)
Từ (1), (2) và (3) suy ra O,H,M thẳng hàng

H cách A cố định một khoảng bằng OA không đổi nên H di chuyển trên đường tròn (A ; AO).
Chúc bạn học tốt

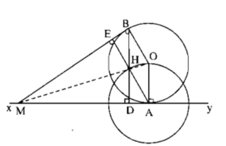
Gọi BD, AE là đường cao của ∆ MAB. Ta có ΔMAE = ∆ MBD (cạnh huyền – góc nhọn) nên ME = MD, ∆ MHE = ∆ MHD (cạnh huyền – cạnh góc vuông) nên ∠ (EMH) = ∠ (DMH). MH và MO đều là tia phân giác của góc AMB nên M, H, O thẳng hàng.

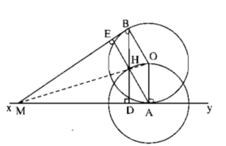
H cách A cố định một khoảng bằng OA không đổi nên H di chuyển trên đường tròn (A; AO).

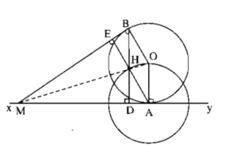
Tứ giác AOBH có BH // OA, AH // OB và OA = OB nên là hình thoi.

Mình không vẽ được hình mong bạn thông cảm
a, Chắc bạn làm rồi
b, Sử dụng tính chất 2 tiếp tuyến cắt nhau
=>\(\hept{\begin{cases}AP=IP\\IQ=BQ\\MA=MB\end{cases}}\)
Khi đó \(P_{MPQ}=MP+AP+MQ+QB=MA+MB=2a\)(đpcm)
c, Vì H là trực tâm của tam giác MAB
=>\(AH\perp MB\)
MÀ \(MB\perp OB\)
=> \(AH//OB\)
CMTT=>\(BH//AO\)
=> tứ giác AHBO là hình bình hành
=>AH=OB=R
MÀ A cố định
=> \(H\in\left(A,R\right)\)cố định
Vậy H thuộc đường tròn tâm A bán kính R cố định
