Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi vận tốc xe của cô Liên là x (km/h, x > 0).
⇒ Vận tốc xe của bác Hiệp là: x + 3 (km/h).
Thời gian bác Hiệp, cô Liên đi là: 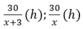
Thời gian đi của bác Hiệp ít hơn thời gian đi của cô Liên là nửa giờ nên ta có phương trình:
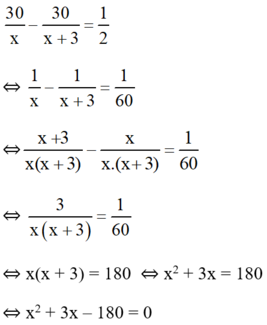
Có a = 1; b = 3; c = -180 ⇒ Δ = 32 – 4.1.(-180) = 729
Phương trình có hai nghiệm:
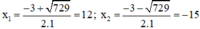
Trong hai nghiệm chỉ có nghiệm x = 12 thỏa mãn điều kiện.
Vậy vận tốc của cô Liên là 12km/h, của bác Hiệp là 15 km/h.

Gọi vận tốc của bác Hiệp là x (km/h), x > 0 khi đó vận tốc của cố Liên là x - 3 (km/h)
Thời gian bác Hiệp đi từ làng lên tỉnh là (giờ).
Thời gian bác Liên đi từ làng lên tỉnh là: (giờ)
Vì bác Hiệp đến trước cô Liên nửa giờ, tức là thời gian đi của bác Hiệp ít hơn thời gian cô Liên nửa giờ nên ta có phương trình: -
=
Giải phương trình:
x(x - 3) = 60x - 60x + 180 hay x2 – 3x - 180 = 0
x1 = 15, x2 = -12
Vì x > 0 nên x2 = -12 không thỏa mãn điều kiện của ẩn.
Trả lời: Vận tốc của bác Hiệp là 15 km/h
Vận tốc của cô Liên là 12 km/h
Bài giải:
Gọi vận tốc của bác Hiệp là x (km/h), x > 0 khi đó vận tốc của cố Liên là x - 3 (km/h)
Thời gian bác Hiệp đi từ làng lên tỉnh là (giờ).
Thời gian bác Liên đi từ làng lên tỉnh là: (giờ)
Vì bác Hiệp đến trước cô Liên nửa giờ, tức là thời gian đi của bác Hiệp ít hơn thời gian cô Liên nửa giờ nên ta có phương trình: -
=
Giải phương trình:
x(x - 3) = 60x - 60x + 180 hay x2 – 3x - 180 = 0
x1 = 15, x2 = -12
Vì x > 0 nên x2 = -12 không thỏa mãn điều kiện của ẩn.
Trả lời: Vận tốc của bác Hiệp là 15 km/h
Vận tốc của cô Liên là 12 km/h
Xem thêm tại: http://loigiaihay.com/bai-47-trang-59-sgk-toan-9-tap-2-c44a6215.html#ixzz4dIBTf3RB

Gọi vận tốc xe đạp là x (x>0)km/h
vận tốc xe máy là x+20 km/h
thời gian xe đạp đi hết quãng đường AB là \(\dfrac{105}{x}\) h
thời gian xe máy đi hết quãng đường AB là \(\dfrac{105}{x+20}\) h
Vì xe máy đến B trược xe đạp 4h nên ta có pt
\(\dfrac{105}{x}-\dfrac{105}{x+20}=4\)
giải pt x=15
vậy vận tốc của xe đạp là 15km/h
=> vận tốc xe máy là 15+20=35km/h
Gọi x (km/h) là vận tốc của người đi xe đạp (x > 0)
\(\Rightarrow x+20\) là vận tốc của người đi xe máy
Thời gian người đi xe đạp đi hết quãng đường AB là: \(\dfrac{105}{x}\) (h)
Thời gian người đi xe máy đi hết quãng đường AB là: \(\dfrac{105}{x+20}\) (h)
Theo đề bài, ta có phương trình:
\(\dfrac{105}{x}-\dfrac{105}{x+20}=4\)
\(\Leftrightarrow105.\left(x+20\right)-105x=4x\left(x+20\right)\)
\(\Leftrightarrow105x+2100-105x=4x^2+80x\)
\(\Leftrightarrow4x^2+80x-2100=0\)
\(\Leftrightarrow x^2+20x-525=0\)
\(\Delta'=10^2-1.\left(-525\right)=625\)
\(\Rightarrow\sqrt{\Delta'}=\sqrt{625}=25\)
\(x_1=\dfrac{-10+25}{1}=15\) (nhận)
\(x_2=\dfrac{-10-25}{1}=-35\) (loại)
Vậy vận tốc của người đi xe đạp là 15 km/h
Vận tốc của người đi xe máy là 15 + 20 = 35 km/h

Gọi x, y (km/h) lần lượt là vận tốc của bác Toàn và cô ba Ngần đi. Điều kiện: x > 0, y > 0.
Vì hai người đi ngược chiều nhau, bác Toàn đi 1 giờ 30 phút, cô ba Ngần đi 2 giờ thì gặp nhau và tổng quãng đường họ đi được bằng khoảng cách từ làng đến thị xã nên ta có phương trình: 1,5x + 2y = 38
Quãng đường bác Toàn đi trong 1 giờ 15 phút là: 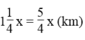
Quãng đường cô ba Ngần đi trong 1 giờ 15 phút là: ![]()
Sau 1 giờ 15 phút, hai người còn cách nhau 10,5km nên ta có phương trình:
![]()
⇔ 5x + 5y = 110
Ta có hệ phương trình:
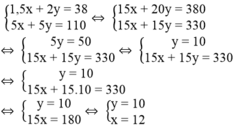
Giá trị của x và y thỏa điều kiện bài toán.
Vậy vận tốc của bác Toàn là 12km/h, vận tốc của cô ba Ngần là 10km/h.

Gọi vận tốc xe của cô Liên là x (km/h, x > 0).
⇒ Vận tốc xe của bác Hiệp là: x + 3 (km/h).
Thời gian bác Hiệp, cô Liên đi là: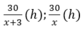
Thời gian đi của bác Hiệp ít hơn thời gian đi của cô Liên là nửa giờ nên ta có phương trình:
Có a = 1; b = 3; c = -180 ⇒ Δ = 3 2 – 4 . 1 . ( - 180 ) = 729
Phương trình có hai nghiệm:
Trong hai nghiệm chỉ có nghiệm x = 12 thỏa mãn điều kiện.
Vậy vận tốc của cô Liên là 12km/h, của bác Hiệp là 15 km/h.