Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi ba số đó là \(x,y,z\). Do ba số là các số hạng thứ hai, thứ 9 và thứ 44 của một cấp số cộng nên:
\(x;y=x+7d;z=x+42d\). (Với d là công sai của cấp số cộng).
Ta có: \(x+y+z=x+x+7d+x+42d=3x+49d=217\).
Mặt khác x, y, z là các số hạng liên tiếp của một cấp số nhân nên:
\(y^2=xz\)\(\Leftrightarrow\left(x+7d\right)^2=x\left(x+42d\right)\)\(\Leftrightarrow-28xd+49d^2=0\)\(\Leftrightarrow7d\left(-4x+7d\right)=0\)\(\Leftrightarrow\left[{}\begin{matrix}d=0\\-4x+7d=0\end{matrix}\right.\).
Với \(d=0\) suy ra \(x=y=z=\dfrac{217}{3}\).
Suy ra: \(n=820:\dfrac{217}{3}=\dfrac{2460}{217}\notin N\).
Với \(4+7d=0\). Ta có hệ:
\(\left\{{}\begin{matrix}4x+7d=0\\3x+49d=217\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}x=7\\d=4\end{matrix}\right.\).
Vậy \(u_1=7-4=3\).
Có \(S_n=\dfrac{\left[2u_1+\left(n-1\right)d\right]n}{2}=\dfrac{\left[2.3+\left(n-1\right)4\right]n}{2}=820\)
\(\Rightarrow n=20\left(tm\right)\).

Theo giả thiết ta có :
\(u_1+u_2=u_1+\frac{1}{4}\left(u_1\right)=24\)
\(\Rightarrow u_1+\frac{1}{4}u_1^2-24=0\)
\(\Leftrightarrow u_1=-12\) V \(u_1=8\)
Vậy có 2 cấp số nhân tương ứng là : 8,16,32,128 hoặc -12,36,-108,-972

Gọi 3 số đó là: \(a,b,c\). Theo bài ra ta có:\(\left\{{}\begin{matrix}a+b+c=114\\b^2=ac\end{matrix}\right.\). (*)
Mặt khác nó lần lượt là số hạng thứ nhất, thứ tư và thứ hai mươi lăm của một cấp số cộng nên: \(a=u_1;b=u_1+3d;c=u_1+24d\). ( với \(u_1\) là số hạng đầu của cấp số cộng, d là công sai).
Thay vào (*) ta có:
\(\left\{{}\begin{matrix}u_1+u_1+3d+u_1+24d=114\\\left(u_1+3d\right)^2=u_1\left(u_1+24d\right)\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}u_1+9d=38\\18u_1d-9d^2=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}u_1+9d=38\\9d\left(2u_1-d\right)=0\end{matrix}\right.\).
Nếu \(d=0\) thì a,b,c là ba số hạng của một cấp số cộng không đổi nên \(a=b=c=\sqrt[3]{114}\).
Nếu \(d\ne0\) suy ra: \(\left\{{}\begin{matrix}u_1+9d=38\\2u_1-d=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}u_1=2\\d=4\end{matrix}\right.\).
Khi đó \(a=2;b=2+3.4=16;c=2+24.3=74\).

a)
Gọi q là công bội của \(\left(u_n\right)\). Ta có:
\(\left\{{}\begin{matrix}u_1+u_1q^4=51\\u_1q+u_1q^5=102\end{matrix}\right.\)\(\Rightarrow\dfrac{u_1+u_1q^4}{u_1q_1+u_1q^5}=\dfrac{51}{102}\)\(\Leftrightarrow\dfrac{1+q^4}{q+q^5}=\dfrac{1}{2}\)\(\Leftrightarrow\dfrac{1+q^4}{q\left(1+q^4\right)}=\dfrac{1}{2}\)\(\Leftrightarrow\dfrac{1}{q}=\dfrac{1}{2}\)\(\Leftrightarrow q=2\).
Suy ra: \(u_1+2^4u_1=51\)\(\Leftrightarrow17u_1=51\)\(\Leftrightarrow u_1=3\).
b) \(S_n=\dfrac{u_1\left(1-q^n\right)}{1-q}=\)\(\dfrac{3\left(1-2^n\right)}{1-2}=3\left(2^n-1\right)=3069\)
\(\Leftrightarrow2^n-1=1023\)\(\Leftrightarrow2^n=1024=2^{10}\)\(\Leftrightarrow n=10\).
Vậy tổng của 10 số hạng đầu tiên bằng 10.
c)
Có \(u_1.q^{n-1}=3.2^{n-1}=12288\)\(\Leftrightarrow2^{n-1}=4096=2^{12}\)\(\Leftrightarrow n-1=12\)\(\Leftrightarrow n=13\).
Vậy số hạng thứ 13 bằng 12 288.


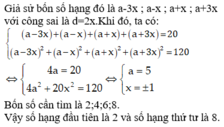
Chọn B
Gọi ba số hạng liên tiếp của cấp số cộng là a - 2x; a ; a+2x với công sai d=2x.
Theo giả thiết ta có:
a − 2 x + a + a + 2 x = − 9 ( a - 2 x ) 2 + a 2 + a + 2 x 2 = 29 ⇔ 3 a = − 9 3 a 2 + 8 x 2 = 29 ⇔ a = − 3 8 x 2 = 2 ⇔ a = − 3 x = ± 1 2
với
x = 1 2 ⇒ u 1 = a − 2 x = − 3 − 2. 1 2 = − 4
với
x = − 1 2 ⇒ u 1 = a − 2 x = − 3 − 2. − 1 2 = − 2
Vậy số hạng đầu tiên là -4 hoặc -2