Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

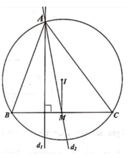
BC và AK cắt BC tại H.Ta có HB=HC (AK là trung trực của BC)
=>HC=BC/2.
AH=√(AC²-CH²);
∆ACH~∆COH (tam giác vuông chung góc nhọn tại O)
=>AH/AC=HC/CO=>CO=AC.HC/AH.
=20.12/√(20²-12²)=20.12/16=15.
Gọi AH, BK là hai đường cao, có AH = 10; BK = 12
thấy hai tgiác CAH và CBK đồng dạng => CA/AH = CB/BK
=> CA/10= 2CH/12 => CA = 2,6.CH (1)
mặt khác áp dụng pitago cho tgiac vuông HAC:
CA² = CH² + AH² (2)
thay (1) vào (2): 2,6².CH² = CH² + 102
=> (2,6² - 1)CH² = 102=> CH = 10 /2,4 = 6,5
=> BC = 2CH = 13 cm

Số phần tử của tập X là C 4 n 3
Gọi A là biến cố: “Chọn được tam giác vuông”
Đa giác đều 4n đỉnh nội tiếp trong đường tròn tâm O có 2n đường chéo qua tâm O.
Mỗi tam giác vuông tạo bởi hai đỉnh nằm trên cùng một đường chéo qua tâm O và một đỉnh trong 4n-2 đỉnh còn lại.
Suy ra số tam giác vuông được tạo thành là C 2 n 1 . C 4 n - 2 1 .
Từ giả thiết suy ra P A = C 2 n 1 . C 4 n - 2 1 C 4 n 3 = 1 13 ⇒ n = 10
Đáp án C

Đáp án là D.
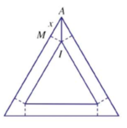
M I = x 3 3 ; S t g = a − 2 x 2 3 4 .
V l t = M I . S t g = a 2 x − 4 a x 2 + 4 x 3 4 ; 0 < x < a 2 .
xét hàm số
f x = 4 x 3 − 4 a x 2 + a 2 x ⇒ f ' x = 12 x 2 − 8 a x + a 2 , cho f ' x = 0 ⇔ x = a 6 x = a 2 l o a i
Thể tích đạt GTLN khi x = a 6 .

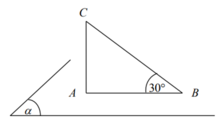
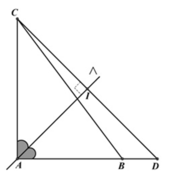
+ Tọa độ B là nghiệm của hệ phương trình
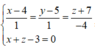
⇒ B 2 ; 3 ; 1
+ Do C ∈ B C nên C 4 + c ; 5 + c ; - 7 - 4 c
Theo giả thiết ![]()
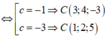
Mà đỉnh C có cao độ âm nên C(3;4;-3 )
+ Gọi A x ; y ; 3 - x ∈ α
Do
A
B
C
=
30
°
nên 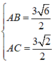

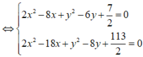
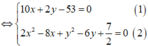
Từ (1) có y = 53 - 10 x 2
Thay vào (2) ta có 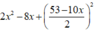
![]()
![]()
![]()
⇒ A 9 2 ; 4 ; - 3 2
Chọn đáp án C.






gọi a,b,c là độ dại 3 cạnh,ha,hb,hc là 3 đường cao tương ứng
ha = 4 và hb = 12,ta tìm hc
+ ta có
S = 1/2*a.ha
=>a = 2S/ha
tương tự
b = 2S/hb
và
c=2S/hc
+ do ABC la 1 tam giác nên
* a + b > c
=> 2S/ha + 2S/hb > 2S/hc
<> 1/hc < 1/4 + 1/12 = 1/3
=> hc > 3
* b + c > a
=> 1/12 + 1/hc > 1/4
<>1/hc > 1/6
=> hc < 6
do hc nguyên nên hc = 4 hoạc hc = 5
cái này hình như thiếu đề