Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn đáp án B
Phương pháp
Chia các TH sau:
TH1: a<b<c.
TH2: a=b<c.
TH3: a<b=c.
TH4: a=b=c.
Cách giải
Gọi số tự nhiên có 3 chữ số là a b c ¯ (0≤a,b,c≤9, a≠0).
=> S có 9.10.10=900 phần tử. Chọn ngẫu nhiên một số từ S => n(Ω)=900
Gọi A là biến cố: “Số được chọn thỏa mãn a≤b≤c”.
TH1: a<b<c. Chọn 3 số trong 9 số từ 1 đến 9, có duy nhất một cách xếp chúng theo thứ tự tăng dần từ trái qua phải nên TH này có C 9 3 số thỏa mãn.
TH2: a=b<c, có C 9 2 số thỏa mãn.
TH3: a<b=c có C 9 2 số thỏa mãn.
TH4: a=b=c có 9 số thỏa mãn.
⇒ n ( A ) = C 9 3 + 2 C 9 2 + 9 = 165
Vậy P ( A ) = 11 60 .

Đáp án A.
Số phần tử của không gian mẫu là n Ω = 36 Gọi A là biến cố thỏa yêu cầu bài toán.
Phương trình x 2 + b x + c = 0 có nghiệm khi và chỉ khi
∆ = b 2 - 4 a c ≥ 0 ⇔ b 2 ≥ 4 a c
Xét bảng kết quả sau (L – loại, không thỏa; N – nhận, thỏa yêu cầu đề bài):
|
1 |
2 |
3 |
4 |
5 |
6 |
1 |
L |
N |
N |
N |
N |
N |
2 |
L |
L |
N |
N |
N |
N |
3 |
L |
L |
L |
N |
N |
N |
4 |
L |
L |
L |
N |
N |
N |
5 |
L |
L |
L |
L |
N |
N |
6 |
L |
L |
L |
L |
N |
N |
Dựa vào bảng kết quả trên ta thấy số kết quả thuận lợi cho A là 19.
Vậy xác suất của biến cố A là P ( A ) = 19 36

4a.
Số tự nhiên là A, ta có:
A = 7m + 5
A = 13n + 4
=>
A + 9 = 7m + 14 = 7(m + 2)
A + 9 = 13n + 13 = 13(n+1)
vậy A + 9 là bội số chung của 7 và 13
=> A + 9 = k.7.13 = 91k
<=> A = 91k - 9 = 91(k-1) + 82
vậy A chia cho 91 dư 82
4b.
Giả sử p là 1 số nguyên tố >3, do p không chia hết cho 3 nên p có dạng 3k + 1 hoặc 3k + 2
Vì p +4 là số nguyên tố nên p không thể có dạng 3k + 2
Vậy p có dạng 3k +1.
=> p + 8 = 3k + 9 chia hết cho 3 nên nó là hợp số.

Số các số thuộc tập S là 7.8.8=448. Số rút ra thoả mãn có dạng
A
B
C
¯
với ![]()
![]() Mỗi cách chọn ra bộ ba số thuộc tập {1,...,9} thu được một bộ số (a; b+1; c+2) tương ứng với một bộ ba số (a;b;c) và cho ta một số có ba chữ số thoả mãn yêu cầu bài toán. Vậy có tất cả
C
9
3
số thoả mãn. Xác suất cần tính bằng
Mỗi cách chọn ra bộ ba số thuộc tập {1,...,9} thu được một bộ số (a; b+1; c+2) tương ứng với một bộ ba số (a;b;c) và cho ta một số có ba chữ số thoả mãn yêu cầu bài toán. Vậy có tất cả
C
9
3
số thoả mãn. Xác suất cần tính bằng 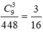
Chọn đáp án C.

Đáp án C
Cách giải:
Xét các số x = a; y = b+1; z = c+2; t = d+3. Vì 1≤a≤b≤c≤d≤9 => 1≤x<y<z<t≤12 (*)
Và mỗi bộ 4 số (x;y;z;t) được chọn từ tập hợp {1;2;3;…;12} ta đều thu được bộ số thỏa mãn
(*). Do đó, số cách chọn 4 số trong 12 số là C 12 4 = 495 số suy ra n(X) = 495
Số phần tử của không gian mẫu là n(Ω) = 9.10.10.10 = 9000
Vậy xác suất cần tính là 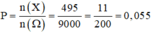

Không gian mẫu n Ω = 9 . 10 3 = 9000 .
Gọi A là biến cố: “số được chọn có dạng a b c d ¯ , trong đó 1 ≤ a ≤ b ≤ c ≤ d ≤ 9 ”
TH1: 1 ≤ a < b < c < d ≤ 9
Chọn ngẫu nhiêu 4 số trong các số từ 1 đến 9 có C 9 4 = 126 cách.
Có duy nhất một cách xếp các chữ số theo thứ tự tăng dần, do đó trường hợp này có 126 số thỏa mãn.
TH2: 1 ≤ a = b < c < d ≤ 9 . Số cần tìm có dạng a a c d ¯ .
Chọn ngẫu nhiên 3 số trong các số từ 1 đến 9 có C 9 3 = 84 cách.
Có duy nhất một cách xếp các chữ số theo thứ tự tăng dần, do đó trường hợp này có 84 số thỏa mãn.
Tương tự như vậy, các trường hợp 1 ≤ a < b = c < d ≤ 9 , 1 ≤ a < b < c = d ≤ 9 mỗi trường hợp cũng có 84 số thỏa mãn.
TH3: 1 ≤ a = b = c < d ≤ 9 . Số cần tìm có dạng a a a d ¯ .
Chọn ngẫu nhiên 2 số trong các số từ 1 đến 9 có C 9 2 = 36 cách.
Có duy nhất một cách xếp các chữ số theo thứ tự tăng dần, do đó trường hợp này có 36 số thỏa mãn.
Tương tự như vậy, các trường hợp 1 ≤ a = b < c = d ≤ 9 , 1 ≤ a < b = c = d ≤ 9 mỗi trường hợp cũng có 36 số thỏa mãn.
TH4: 1 ≤ a = b = c = d ≤ 9 . Số cần tìm có dạng a a a a ¯ . Có 9 số thỏa mãn.
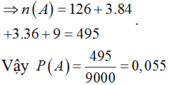
Chọn B.