Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Độ dài đáy CD là: 4 x 2 = 8 cm
Diện tích hình thang cân ABCD là: (4+8)x3:2 = 18 cm2
Độ dài đáy CD là:
4 x 2 = 8 (cm)
Diện tích hình thang cân ABCD là:
3 x ( \(\dfrac{4+8}{2}\)) = 18 (cm2)
Đáp số: 18 cm2

Độ dài cạnh CD là:
4.2=8(cm)
S hình thang cân là:
(4+8).3:2=18(cm2)
Đ/S:.....
Lời giải: Độ dài đáy CD gấp đôi độ dài đáy AB nên độ dài đáy CD là: 4 . 2 = 8 (cm) Ta có: AB = 4 cm; CD = 8 cm; AH = 3 cm. Do đó diện tích hình thang cân ABCD là: Cho hình thang cân ABCD có độ dài đáy AB bằng 4 cm, độ dài đáy CD gấp đôi độ dài đáy AB Vậy diện tích hình thang cân ABCD là 18cm2

a: \(CD=3\cdot AB=3\cdot4=12\left(cm\right)\)
b: Diện tích hình thang ABCD là:
\(S_{ABCD}=\dfrac{1}{2}\cdot\left(AB+CD\right)\cdot AH=\dfrac{1}{2}\cdot3\cdot\left(12+4\right)=\dfrac{3}{2}\cdot16=24\left(cm^2\right)\)
c: ABCD là hình thang cân
=>AD=BC
mà AD=5cm
nên BC=5cm
Chu vi hình thang ABCD là:
\(C_{ABCD}=AB+BC+CD+DA\)
=5+5+4+12
=10+16
=26(cm)

Bài làm:
Tổng độ dài hai đáy là
10.2=20(cm)
Độ dài đáy AB là
20-12=8(cm)
Chiều cao của hình thang là
8-3=5(cm)
Diện tích hình thang cân ABCD là
(12+8).5:2 =50(cm2)
Dấu . là nhân nha!!
cm2 là cm vuông!!

Độ dài đáy CD là: 4 x 2 = 8 cm
Diện tích hình thang cân ABCD là: (4+8)x3:2 = 18 cm2
Độ dài đáy CD là: 4 x 2 = 8 cm Diện tích hình thang cân ABCD là: (4+8)x3:2 = 18 cm2

AB=CD-6=16-6=10(cm)
\(AD=\dfrac{AB}{2}=5\left(cm\right)\)
Vì ABCD là hình thang cân
nên \(AD=BC=5\left(cm\right)\)
Chu vi hình thang cân ABCD là:
\(AB+AD+CD+BC=5+5+10+16=36\left(cm\right)\)
Diện tích hình thang cân ABCD là:
\(S_{ABCD}=\dfrac{1}{2}\cdot AH\cdot\left(AB+CD\right)\)
\(=\dfrac{1}{2}\cdot4\cdot\left(10+16\right)=2\cdot26=52\left(cm^2\right)\)
Cạnh AB dài:
16 - 6 = 10 (cm)
Cạnh AD dài:
10 : 2 = 5 (cm)
Chu vi hình thang cân ABCD:
16 + 10 + 5 + 5 = 36 (cm)
Diện tích hình thang:
(16 + 10) × 4 : 2 = 52 (cm²)

PQ=7*2=14cm
\(S_{MNPQ}=\dfrac{1}{2}\cdot\left(7+14\right)\cdot4=2\cdot21=42\left(cm^2\right)\)
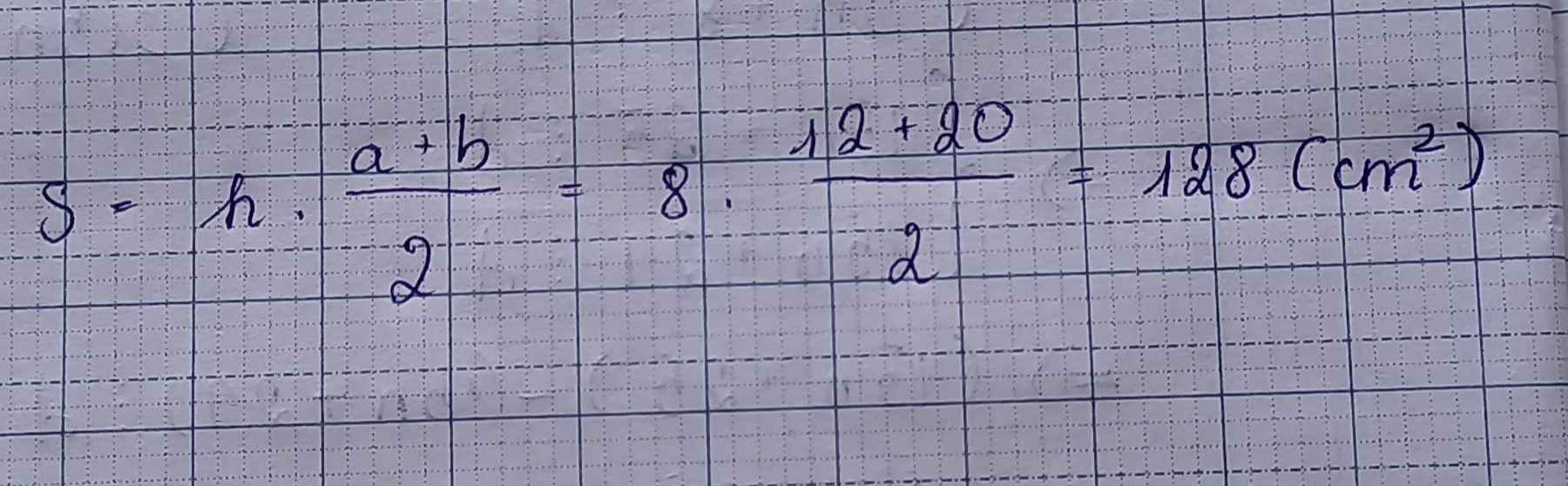
Bài 1:
\(S=\dfrac{12+20}{2}\cdot8=16\cdot8=128\left(cm^2\right)\)