Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) Ta có: AC2 = AB2 + BC2 (Pytago) = 32 + 32 = 18(cm)
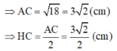
Lại có: SH2 = SC2 - HC2 (Pytago)
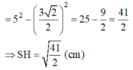
b) Gọi K là trung điểm của BC
Ta có: SK2 = SH2 + HK2 (Pytago)
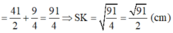
![]()
![]()
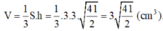

Gọi M là trung điểm của AB:
\(\Rightarrow MA=MB=\dfrac{AB}{2}=\dfrac{10}{2}=5\left(cm\right)\)
Do SM là ⊥ AB nên ΔSAM vuông tại M áp dụng định lý Py-ta-go ta có:
\(SA^2=SM^2+MA^2\)
\(\Rightarrow13^2=SM^2+5^2\)
\(\Rightarrow SM=\sqrt{13^2-5^2}=12\left(cm\right)\)
Nữa chu vi đáy của hình chóp tứ giác đều:
\(p=\dfrac{4\cdot10}{2}=20\left(cm\right)\)
Diện tích xung quanh của chóp tứ giác đều là:
\(S_{xq}=p\cdot d=20\cdot12=240\left(cm^2\right)\)
Ảnh tham khảo:
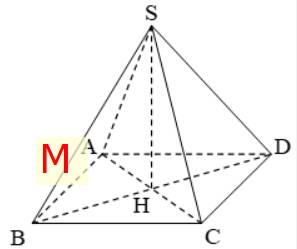
Gọi x (cm) là đường cao của mặt bên:
Ta có:
x² = 13² - 5² = 144
x = 12 (cm)
Diện tích xung quanh của hình chóp:
4 . 12 . 10 : 2 = 240 (cm²)

Lời giải:
Xét tam giác $SAB$ có $SA=SB=10$, $AB=12$
Kẻ $SH\perp AB$ thì $H$ là trung điểm của $AB$.
$\Rightarrow AH=6$ (cm)
Theo định lý Pitago:
$SH=\sqrt{SA^2-AH^2}=\sqrt{10^2-6^2}=8$ (cm)
$S_{SAB}=\frac{SH.AB}{2}=\frac{8.12}{2}=48$ (cm vuông)
$S_{xq}=3S_{SAB}=3.48=144$ (cm vuông)

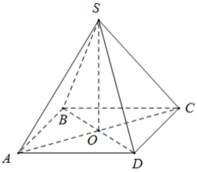
Ta có ABCD là hình vuông, khi đó nửa chu vi bằng:
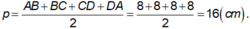
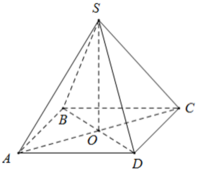
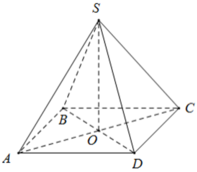
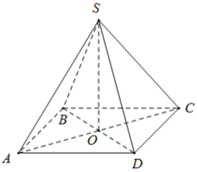
+ BD = AC = √ (82 + 82) = 8√ 2 ( cm ) ⇒ AO = BO = CO = DO = 4√ 2 ( cm )
Do đó:
+ Diện tích xung quanh của hình chóp đều là Sxq = p.d = p.OB = 16.4√ 2 = 64√ 2 ( cm2 ).
+ Diện tích toàn phần của hình chóp đều là
Stp = Sxq + SABCD = 64√ 2 + 82 = 64 + 64√ 2 ( cm2 )
+ Thể tích của hình chóp đều là V = 1/3S.h = 1/3.SABCD.SO = 1/3.82.10 = 640/3( cm3 )
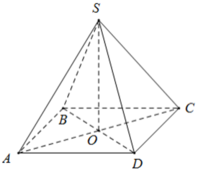
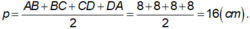

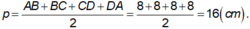

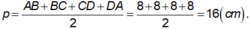

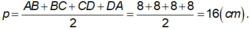

ai biết làm k giúy mk vs mai mk ktra 1 tiết r