b) Tính: (1 - 1 2 ) x (1 - 1 3 ) x (1 - 1 4 ) x (1 -...

b) Tính: (1 - 1 2 ) x (1

NN

Nguyễn Ngọc An

6 tháng 4 2017 - olm

Tính:a) ( 1- \(\frac{1}{2}\)) x (1- \(\frac{1}{3}\)) x (1- \(\frac{1}{4}\)) x (1- \(\frac{1}{5}\)) x..........x ( 1- \(\frac{1}{99}\))x ( 1- \(\frac{1}{100}\))b) ( ( 1+ \(\frac{1}{2}\)) x (1+ \(\frac{1}{3}\)) x (1+ \(\frac{1}{4}\)) x (1+ \(\frac{1}{5}\)) x..........x ( 1+ \(\frac{1}{99}\))x (...

Đọc tiếp

#Hỏi cộng đồng OLM #Toán lớp 5

22

NT

Nguyễn Tiến Dũng

6 tháng 4 2017

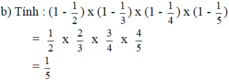
a)\(=\frac{1}{2}.\frac{2}{3}.\frac{3}{4}.\frac{4}{5}......\frac{99}{100}\)

\(=\frac{1.2.3.4.....99}{2.3.4.5.6.....100}\)

\(=\frac{1}{100}\)

b) Tương tự như câu a

Đúng(0)

NN

Nguyễn Ngọc An

6 tháng 4 2017

Ra kết quả phần b là \(\frac{101}{2}\) đúng hông?

Đúng(0)

A

✎﹏🅷ạ🅽🅷︵❣🅿🅷ú🅲︵❣Đé🅾︵❣🅲ó︵❣Đâ🆄︵❣✔

21 tháng 6 2018 - olm

tính nhanh

a, \(\frac{3}{5}\)+25-\(\frac{1}{5}\)

b, 13x3x32,27+67,63x39

c, (1-\(\frac{1}{2}\))x(1-\(\frac{1}{3}\))x(1-\(\frac{1}{4}\)) x......x(1-\(\frac{1}{100}\))

#Hỏi cộng đồng OLM #Toán lớp 5

3

DL

Dương Lam Hàng

21 tháng 6 2018

a) \(\frac{3}{5}+25-\frac{1}{5}=\left(\frac{3}{5}-\frac{1}{5}\right)+25=\frac{2}{5}+25=\frac{2}{5}+\frac{125}{5}=\frac{127}{5}\)

b) \(13\times3\times32,27+67,63\times39=39\times32,27+67,63\times39\)

\(=39\times\left(32,27+67,63\right)\)

\(=39\times99,9=3196,8\)

(Bạn xem lại đề nhé)

c) \(\left(1-\frac{1}{2}\right)\times\left(1-\frac{1}{3}\right)\times\left(1-\frac{1}{4}\right)\times....\times\left(1-\frac{1}{100}\right)\)

\(=\frac{1}{2}\times\frac{2}{3}\times\frac{3}{4}\times.....\times\frac{99}{100}\)

\(=\frac{1\times2\times3\times...\times99}{2\times3\times4\times....\times100}=\frac{1}{100}\)

Đúng(0)

L

➻❥L҉ê❄Q҉U҉A҉N҉G҉❄T҉U҉ấN҉❄K҉I҉ệT҉ঔ

21 tháng 6 2018

a, \(\frac{3}{5}+25-\frac{1}{5}=\frac{127}{5}\)

b, \(\text{13 x 3 x 32,27 + 67,63 x 39 =}3896,1\)

............................

thank for watching me do homework

Đúng(0)

NT

Nguyễn Thanh Ngân

22 tháng 6 2015 - olm

Tính nhanh : \(\frac{1}{2}x\frac{1}{2}+\frac{1}{2}x\frac{1}{3}+\frac{1}{3}x\frac{1}{4}+\frac{1}{4}x\frac{1}{5}+\frac{1}{5}x\frac{1}{6}\)

#Hỏi cộng đồng OLM #Toán lớp 5

3

ST

sat thu dam lay

22 tháng 6 2015

???????????????????????????????????????????????????????????????????????????^_^

Đúng(0)

TD

Trần Đức Thắng

22 tháng 6 2015

= 1/1 - 1/2 + 1/2 - 1/3 +.. + 1/5 - 1/6

= 1/1 - 1/6

= 5/6

Đúng(0)

AC

anh chàng đẹp trai

3 tháng 6 2019 - olm

Bài1:Tính giá trị biểu thức sau:A=\(\left(6:\frac{3}{5}-1\frac{1}{6}x\frac{6}{7}\right):\left(4\frac{1}{5}x\frac{10}{11}+5\frac{2}{11}\right)\)Bài 2: Tính giá trị biểu thức:B= \(\left(1-\frac{1}{2}\right)x\left(1-\frac{1}{3}\right)x\left(1-\frac{1}{4}\right)x\left(1-\frac{1}{5}\right)...\left(1-\frac{1}{2003}\right)x\left(1-\frac{1}{2004}\right)\)ai xong sẽ có tích , phải làm giải từng bước ra...

Đọc tiếp

#Hỏi cộng đồng OLM #Toán lớp 5

5

LT

Lê Tài Bảo Châu

3 tháng 6 2019

Bài 2:

\(B=\left(1-\frac{1}{2}\right).\left(1-\frac{1}{3}\right).\left(1-\frac{1}{4}\right).......\left(1-\frac{1}{2004}\right)\)

\(=\frac{1}{2}.\frac{2}{3}.\frac{3}{4}....\frac{2003}{2004}\)

\(=\frac{1}{2004}\)

Đúng(0)

F

FAH_buồn

3 tháng 6 2019

Bài 2

=1/2 x 2/3 ... x 2003/2004

=1/2004

Đúng(0)

DN

Đỗ Nguyễn Quỳnh Anh

28 tháng 5 2019 - olm

Bài 7 :Tính nhanh:

a) 2/3:5/7x5/7:2/3+1934

b) (30 : \(7\frac{1}{2}\)+0,5 x 3 -1,5 ) x (\(4\frac{1}{2}-\frac{9}{2}\)) : ( 14,5 x 1000 )

c) (1999 x 1998 + 1998 x 1997 ) x ( 1 + 1/2 : 1\(\frac{1}{2}\)-1\(\frac{1}{3}\))

#Hỏi cộng đồng OLM #Toán lớp 5

1

DL

Duc Loi

28 tháng 5 2019

b) \(\frac{1}{1000}+\frac{13}{1000}+\frac{25}{1000}+...+\frac{87}{1000}+\frac{99}{1000}\)

\(=\frac{1+13+25+...+85+97}{1000}=\frac{\left(97+1\right).\left[\left(97-1\right):12+1\right]:2}{1000}\)

\(=\frac{49.9}{1000}=\frac{441}{1000}.\) ( Đề bài sai nhé bạn tử số : 1; 13; 25; 37; 49 ; 61; 73; 85 ; 97. )

Đúng(0)

PV

pham van trieu

8 tháng 8 2016 - olm

a,70/3 —(x+4 1/5)=16

b,x:1/2+1 1/3=2 4/5

c,1/2+x:3=10/3

đ, (2x x—1)x(3—x)=0

#Hỏi cộng đồng OLM #Toán lớp 5

1

OI

o0o I am a studious person o0o

8 tháng 8 2016

\(\frac{70}{3}-\left(x+4\frac{1}{5}\right)=16\)

\(\Rightarrow x+4\frac{1}{5}=\frac{22}{3}\)

\(\Rightarrow x+\frac{21}{5}=\frac{22}{3}\)

\(\Rightarrow x=\frac{22}{3}-\frac{21}{5}\)

\(\Rightarrow x=\frac{47}{15}\)

Đúng(0)

MK

minh Khuat

11 tháng 12 2015 - olm

Tính nhanh :

a : 1/2 x 2/3 x 3/4 x....x99/100

b : \(1\frac{1}{2}\) x \(1\frac{1}{3}\)x \(1\frac{1}{4}\)x \(1\frac{1}{5}\)x \(1\frac{1}{6}\)x \(1\frac{1}{7}\) x \(1\frac{1}{8}\)

#Hỏi cộng đồng OLM #Toán lớp 5

1

PT

Pham Thanh Phuong

11 tháng 12 2015

b:

3/2 x 4/3 x 5/4 x ......... x 8/7 x 9/8

Ta loai bo so giong nhau o TS va MS

Ta duoc 9/2

Đúng(0)

NA

Ngọc Ánh

7 tháng 8 2016 - olm

\(A=\left(6:\frac{3}{5}-1\frac{1}{6}x\frac{6}{7}\right):\left(4\frac{1}{5}x\frac{10}{11}+5\frac{2}{11}\right)\)\(B=\left(1-\frac{1}{2}\right)x\left(1-\frac{1}{4}\right)x.......x\left(1-\frac{1}{2015}\right)x\left(1-\frac{1}{2016}\right)\)

\(C=5\frac{9}{10}:\frac{3}{2}-\left(2\frac{1}{3}x4\frac{1}{2}-2x2\frac{1}{3}\right):\frac{7}{4}\)

#Hỏi cộng đồng OLM #Toán lớp 5

0

NT

Nguyễn Thái Hưng

15 tháng 8 2016 - olm

Tính biểu thức sau:

L=(1-1/2)x(1-1/3)x(1-1/4)x(1-1/5)x ..................x(1-1/2003)x(1-1/2004)

#Hỏi cộng đồng OLM #Toán lớp 5

2

DL

Dương Lam Hàng

15 tháng 8 2016

Ta có: \(L=\left(1-\frac{1}{2}\right).\left(1-\frac{1}{3}\right)....\left(1-\frac{1}{2004}\right)\)

\(\Rightarrow L=\frac{1}{2}.\frac{2}{3}.\frac{3}{4}.....\frac{2003}{2004}\)\(=\frac{1.2.3.4....2003}{2.3.4.....2004}=\frac{1}{2004}\)

VẬY \(L=\frac{1}{2004}\)

Đúng(0)

SK

Sherlockichi Kazukosho

15 tháng 8 2016

\(L=\left(1-\frac{1}{2}\right)x\left(1-\frac{1}{3}\right)x\left(1-\frac{1}{4}\right)x.....x\left(1-\frac{1}{2003}\right)\)

\(L=\frac{1}{2}x\frac{2}{3}x\frac{3}{4}x.....x\frac{2002}{2003}\)

\(L=\frac{1x2x3x4x....x2002}{2x3x4x5x.....x2003}=\frac{1}{2003}\)

Đúng(0)

HT

~Huyền team 2k8~

20 tháng 12 2018 - olm

tính

(1-\(\frac{1}{2}\)) x (1-\(\frac{1}{3}\)) x( 1-\(\frac{1}{4}\)) x (1-\(\frac{1}{5}\)) x (1-\(\frac{1}{6}\))

#Hỏi cộng đồng OLM #Toán lớp 5

1

NH

Nguyễn Hoàng Anh Phong

20 tháng 12 2018

\(\left(1-\frac{1}{2}\right).\left(1-\frac{1}{3}\right).\left(1-\frac{1}{4}\right).\left(1-\frac{1}{5}\right)\)

\(=\frac{1}{2}\cdot\frac{2}{3}\cdot\frac{3}{4}\cdot\frac{4}{5}\)

\(=\frac{1}{5}\)

Đúng(0)

Chúng tôi đề xuất

Tài nguyên

Ứng dụng mobile

Bảng xếp hạng

Các khóa học có thể bạn quan tâm

Yêu cầu VIP