Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1,\(P=n^4-4-\left(n^2-2\right)\left(5n-9\right)\)
\(P=\left(n^2+2\right)\left(n^2-2\right)-\left(n^2-2\right)\left(5n-9\right)\)
\(P=\left(n^2-2\right)\left(n^2+2-5n+9\right)\)
\(P=\left(n^2-2\right)\left(n^2-5n+7\right)\)
Vậy......

\(1,\\ b,=\left(x-6\right)\left(x+6\right)\\ 3,\\ x^2-2x+1=25\\ \Leftrightarrow\left(x-1\right)^2-25=0\\ \Leftrightarrow\left(x-6\right)\left(x+4\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=6\\x=-4\end{matrix}\right.\)

Điều kiện xác định của phân thức: n ≠ 2
Ta có:
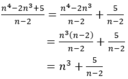
Vậy để N nguyên thì 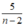 nguyên ⇒ n – 2 là ước của 5;
Ư
(
5
)
=
-
1
;
1
;
-
5
;
5
nguyên ⇒ n – 2 là ước của 5;
Ư
(
5
)
=
-
1
;
1
;
-
5
;
5
n - 2= -1 ⇒ n =1;
n – 2 = 1 ⇒ n =3;
n – 2 = -5 ⇒ n = - 3;
n – 2 = 5 ⇒ n = 7;
vì n ∈ N nên n = 1; n = 3; n = 7
Vậy với n ∈ { 1; 3; 7} thì 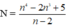 có giá trị là số nguyên
có giá trị là số nguyên

x đầu ở đa thức A là x^3 chăng?
a/ \(A=x^3-5x^2+8x-4\)
\(=\left(x^3-x^2\right)+\left(-4x^2+4\right)+\left(8x-8\right)\)
\(=x^2\left(x-1\right)-4\left(x-1\right)\left(x+1\right)+8\)
\(=\left(x-1\right)\left(x^2-4x-4\right)=\left(x-1\right)\left(x-2\right)^2\)
b/ \(B=\dfrac{x^5}{30}-\dfrac{x^3}{6}+\dfrac{2x}{15}\)
\(=\dfrac{x^5}{30}-\dfrac{5x^3}{30}+\dfrac{4x}{30}\)
\(=\dfrac{x\left(x^4-5x^2+4\right)}{30}\)
\(=\dfrac{x\left(x^4-x^2-4x^2+4\right)}{30}\)
\(=\dfrac{x\left(x+2\right)\left(x-1\right)\left(x+1\right)\left(x-2\right)}{30}\)
a)\(n^4+4\)
\(=\left(n^4-2n^3+2n^2\right)+\left(2n^3-4n^2+4n\right)+\left(2n^2-4n+4\right)\)
\(=n^2\left(n^2-2n+2\right)+2n\left(n^2-2n+2\right)+2\left(n^2-2n+2\right)\)
\(=\left(n^2-2n+2\right)\left(n^2+2n+2\right)\)
Làm nốt
Ta có:\(A=\left(n^2-2n+2\right)\left(n^2+2n+2\right)\)
Để A là số nguyên tố nên 1 trong 2 thừa số phải bằng 1 và số còn lại phải là số nguyên tố
Do \(n^2-2n+2< n^2+2n+2\)nên \(n^2-2n+2=1\)
\(\Leftrightarrow n^2-2n+1=0\)
\(\Leftrightarrow\left(n-1\right)^2=0\)
\(\Leftrightarrow n=1\)
Thay n=1 vào \(n^2+2n+2\) ta được \(n^2+2n+2=5\) là số nguyên tố
Vậy n=1