Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Xét phương trình tiếp tuyến tổng quát có dạng:
\(y=\left(6x_0+3x_0^2\right)\left(x-x_0\right)+3x_0^2+x_0^3\)
có 3 tiếp tuyến đi qua A(a,0) nên phương trình \(\left(6x_0+3x_0^2\right)\left(a-x_0\right)+3x_0^2+x_0^3=0\) có 3 nghiệm
\(PT\Leftrightarrow\orbr{\begin{cases}x_0=0\\2x_0^2+3\left(1-a\right)x_0+6a=0\end{cases}}\)
Vậy có 1 pttt là y=0
do đó để có hai tiếp tuyến vuông góc thì \(2x_0^2+3\left(1-a\right)x_0+6a=0\) có hia nghiệm \(x_1,x_2\text{ thỏa mãn}\)
\(\left(6x_1+3x_1^2\right)\left(6x_2+3x_2^2\right)=-1\)mà áp dung Viet ta có \(\hept{\begin{cases}x_1+x_2=\frac{3a-3}{2}\\x_1x_2=3a\end{cases}}\)
Nên \(36x_1x_2+18x_1x_2\left(x_1+x_2\right)+9x_1^2x_2^2=-1\Leftrightarrow126a+81a\left(a-1\right)+81a^2=-1\)
từ đây mình giải được a nhé
Xét phương trình tiếp tuyến tổng quát có dạng:
y=(6x0+3x02)(x−x0)+3x02+x03
có 3 tiếp tuyến đi qua A(a,0) nên phương trình (6x0+3x02)(a−x0)+3x02+x03=0 có 3 nghiệm
PT⇔[
| x0=0 |
| 2x02+3(1−a)x0+6a=0 |
Vậy có 1 pttt là y=0
do đó để có hai tiếp tuyến vuông góc thì 2x02+3(1−a)x0+6a=0 có hia nghiệm x1,x2 thỏa mãn
(6x1+3x12)(6x2+3x22)=−1mà áp dung Viet ta có {
| x1+x2=3a−32 |
| x1x2=3a |
Nên 36x1x2+18x1x2(x1+x2)+9x12x22=−1⇔126a+81a(a−1)+81a2=−1


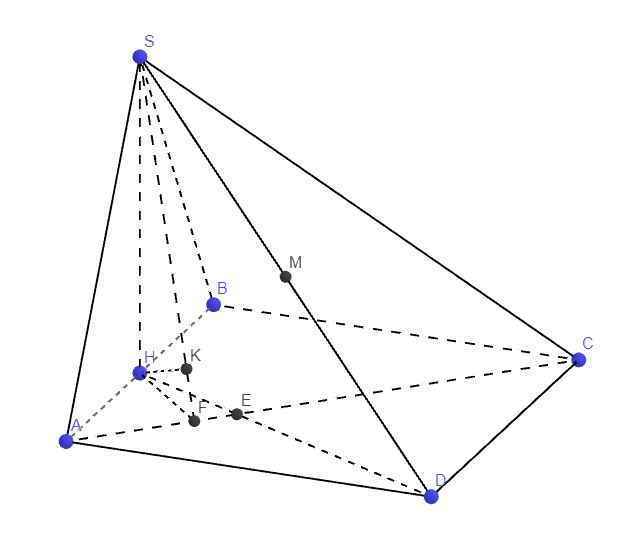
Gọi H là trung điểm AB, có lẽ từ 2 câu trên ta đã phải chứng minh được \(SH\perp\left(ABCD\right)\)
Do \(\left\{{}\begin{matrix}DM\cap\left(SAC\right)=S\\MS=\dfrac{1}{2}DS\end{matrix}\right.\) \(\Rightarrow d\left(M;\left(SAC\right)\right)=\dfrac{1}{2}d\left(D;\left(SAC\right)\right)\)
Gọi E là giao điểm AC và DH
Talet: \(\dfrac{HE}{DE}=\dfrac{AH}{DC}=\dfrac{1}{2}\Rightarrow HE=\dfrac{1}{2}DE\)
\(\left\{{}\begin{matrix}DH\cap\left(SAC\right)=E\\HE=\dfrac{1}{2}DE\end{matrix}\right.\) \(\Rightarrow D\left(H;\left(SAC\right)\right)=\dfrac{1}{2}d\left(D;\left(SAC\right)\right)=d\left(M;\left(SAC\right)\right)\)
Từ H kẻ HF vuông góc AC (F thuộc AC), từ H kẻ \(HK\perp SF\)
\(\Rightarrow HK\perp\left(SAC\right)\Rightarrow HK=d\left(H;\left(SAC\right)\right)\)
ABCD là hình vuông \(\Rightarrow\widehat{HAF}=45^0\Rightarrow HF=AH.sin45^0=\dfrac{a\sqrt{2}}{4}\)
\(SH=\dfrac{a\sqrt{3}}{2}\), hệ thức lượng:
\(HK=\dfrac{SH.HF}{\sqrt{SH^2+HF^2}}=\dfrac{a\sqrt{21}}{14}\)
\(\Rightarrow d\left(M;\left(SAC\right)\right)=\dfrac{a\sqrt{21}}{14}\)


3.
\(4sinx+cosx+2cos\left(x+\dfrac{\pi}{3}\right)=2\)
\(\Leftrightarrow4sinx+cosx+cosx-\sqrt{3}sinx=2\)
\(\Leftrightarrow\left(4-\sqrt{3}\right)sinx+2cosx=2\)
\(\Leftrightarrow\sqrt{23-4\sqrt{3}}\left(\dfrac{4-\sqrt{3}}{\sqrt{23-4\sqrt{3}}}sinx+\dfrac{2}{\sqrt{23-4\sqrt{3}}}cosx\right)=2\)
\(\Leftrightarrow cos\left(x-arccos\dfrac{2}{\sqrt{23-4\sqrt{3}}}\right)=\dfrac{2}{\sqrt{23-4\sqrt{3}}}\)
\(\Leftrightarrow x-arccos\dfrac{2}{\sqrt{23-4\sqrt{3}}}=\pm arccos\dfrac{2}{\sqrt{23-4\sqrt{3}}}+k2\pi\)
\(\Leftrightarrow\left[{}\begin{matrix}x=2arccos\dfrac{2}{\sqrt{23-4\sqrt{3}}}+k2\pi\\x=k2\pi\end{matrix}\right.\)
4.
\(sinx+2cos\left(x+\dfrac{\pi}{3}\right)+4sin\left(x+\dfrac{\pi}{6}\right)+cosx=4\)
\(\Leftrightarrow sinx+cosx-\sqrt{3}sinx+2\sqrt{3}sinx+2cosx+cosx=4\)
\(\Leftrightarrow\left(1+\sqrt{3}\right)sinx+4cosx=4\)
\(\Leftrightarrow\sqrt{20+2\sqrt{3}}\left(\dfrac{1+\sqrt{3}}{\sqrt{20+2\sqrt{3}}}sinx+\dfrac{4}{\sqrt{20+2\sqrt{3}}}cosx\right)=4\)
\(\Leftrightarrow cos\left(x-arccos\dfrac{4}{\sqrt{20+2\sqrt{3}}}\right)=\dfrac{4}{\sqrt{20+2\sqrt{3}}}\)
\(\Leftrightarrow x-arccos\dfrac{4}{\sqrt{20+2\sqrt{3}}}=\pm arccos\dfrac{4}{\sqrt{20+2\sqrt{3}}}+k2\pi\)
\(\Leftrightarrow\left[{}\begin{matrix}x=2arccos\dfrac{4}{\sqrt{20+2\sqrt{3}}}+k2\pi\\x=k2\pi\end{matrix}\right.\)

13 . b ) SH \(\perp\left(ABCD\right)\Rightarrow SH\perp DI\) .
Dễ dàng c/m : DI \(\perp HC\) . Suy ra : \(DI\perp\left(SHC\right)\Rightarrow DI\perp SC\) ( đpcm )
Thấy : \(\left(SBC\right)\cap\left(ABCD\right)=BC\)
C/m : SB \(\perp BC\) . Thật vậy : \(BC\perp AB;BC\perp SH\Rightarrow BC\perp\left(SAB\right)\Rightarrow BC\perp SB\)
Có : \(AB\perp BC\) nên : \(\left(\left(SBC\right);\left(ABCD\right)\right)=\left(SB;AB\right)=\widehat{SBA}=60^o\)

1.
Hàm số xác định khi:
\(\left\{{}\begin{matrix}sinx\ne0\\cosx-1\ne0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x\ne k\pi\\x\ne k2\pi\end{matrix}\right.\Leftrightarrow x\ne k\pi\)
2.
Hàm số xác định khi:
\(cosx\ne-1\Leftrightarrow x\ne\pi+k2\pi\)
3.
\(cosx+1\ge0\Rightarrow\) Hàm số xác định với mọi x
4.
Hàm số xác định khi:
\(x^2-1\ne0\Leftrightarrow x\ne\pm1\)
5.
Hàm số xác định khi:
\(sin^2x-cos^2x\ne0\Leftrightarrow-cos2x\ne0\Leftrightarrow2x\ne\dfrac{\pi}{2}+k\pi\Leftrightarrow x\ne\dfrac{\pi}{4}+\dfrac{k\pi}{2}\)
6.
Hàm số xác định khi:
\(cos3x-cosx\ne0\Leftrightarrow cos3x\ne cosx\Leftrightarrow3x\ne\pm x+k2\pi\Leftrightarrow\left[{}\begin{matrix}x\ne k\pi\\x\ne\dfrac{k\pi}{2}\end{matrix}\right.\)
\(sin^2x-cos^2x\ne0\Leftrightarrow-cos2x\ne0\Leftrightarrow2x\ne\dfrac{\pi}{2}+k\pi\Leftrightarrow x\ne\dfrac{\pi}{4}+\dfrac{k\pi}{2}\)






 em đang bí quá, giúp em với ạ, đề thi thử toán 11
em đang bí quá, giúp em với ạ, đề thi thử toán 11


