
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



A= 3/4 +2/5-7/5+5/4
= (3/4 + 5/4) + (2/5-7/5)
= 2 + (-1)
= 1

Gọi x,y,z là số học sinh khối 6, 7, 8
(x,y,z>0, đvị là học sinh)
Đã biết khối học sinh lớp 8 ít hơn số hs khối 6 là 120 hs
x-z=120
x, y, z tỉ lệ với 8, 7, 5
x/8=y/7=z/5
Áp dụng tính chất dãy tỉ số bằng nhau có:
x/8=y/7=z/5= x-z/8-5=120/3=40
=> x/8= 40 => x=40.8=320 => số hs khối 6 là 320 hs
y/7= 40 y=40.7= 280 số hs khối 7 là 280 hs
z/5= 40 z=40.5=200 số hs khối 8 là 200 hs

1: A=-1/2*xy^3*4x^2y^2=-2x^3y^5
Bậc là 8
Phần biến là x^3;y^5
Hệ số là -2
2:
a: P(x)=3x+4x^4-2x^3+4x^2-x^4-6
=3x^4-2x^3+4x^2+3x-6
Q(x)=2x^4+4x^2-2x^3+x^4+3
=3x^4-2x^3+4x^2+3
b: A(x)=P(x)-Q(x)
=3x^4-2x^3+4x^2+3x-6-3x^4+2x^3-4x^2-3
=3x-9
A(x)=0
=>3x-9=0
=>x=3

Ta có \(Q\left(1\right)=5-5+a^2-a=0\Leftrightarrow a\left(a-1\right)=0\Leftrightarrow\left[{}\begin{matrix}a=0\\a=1\end{matrix}\right.\)

a) Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=3^2+4^2=25\)
hay BC=5(cm)
b) Xét ΔABC có AB<AC<BC(3cm<4cm<5cm)
mà góc đối diện với cạnh AB là \(\widehat{ACB}\)
và góc đối diện với cạnh AC là \(\widehat{ABC}\)
và góc đối diện với cạnh BC là \(\widehat{BAC}\)
nên \(\widehat{ACB}< \widehat{ABC}< \widehat{BAC}\)
Xét ΔABC có
HB là hình chiếu của AB trên BC
HC là hình chiếu của AC trên BC
AB<AC
Do đó: HB<HC
c) Xét ΔCAB vuông tại A và ΔCAD vuông tại A có
CA chung
AB=AD(gt)
Do đó: ΔCAB=ΔCAD(hai cạnh góc vuông)
Suy ra: CB=CD(hai cạnh tương ứng)
Xét ΔCBD có CB=CD(cmt)
nên ΔCBD cân tại C(Định nghĩa tam giác cân)

Cho em xin đề toan hình 1 tiết lớp 7 với ạ !! Em cần gấp !!!!!!! Mọi người giúp em !! Rồi giải câu đó ra cho em luôn ạ !! EM cảm ơn nhiều <3
Câu 1:(1,5 điểm)
Trong hình sau, cho a // b tính 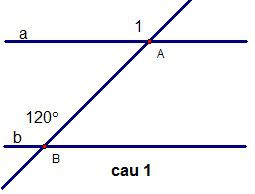
Câu 2:(1,5 điểm)
Cho đoạn thẳng AB dài 3cm. Vẽ đường trung trực của đoạn thẳng AB.
Câu 3:(3 điểm)
Cho a // b; c a.
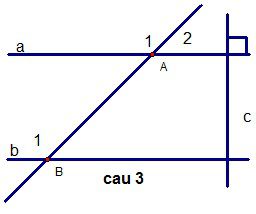
Đường thẳng c có vuông góc với đường thẳng b không ? vì sao?
Cho . tính
,
Câu 4:(4 điểm)
Hình vẽ sau đây cho biết : a // b, ,
.
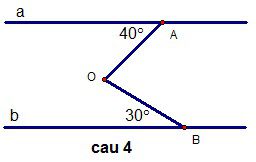
Tính .

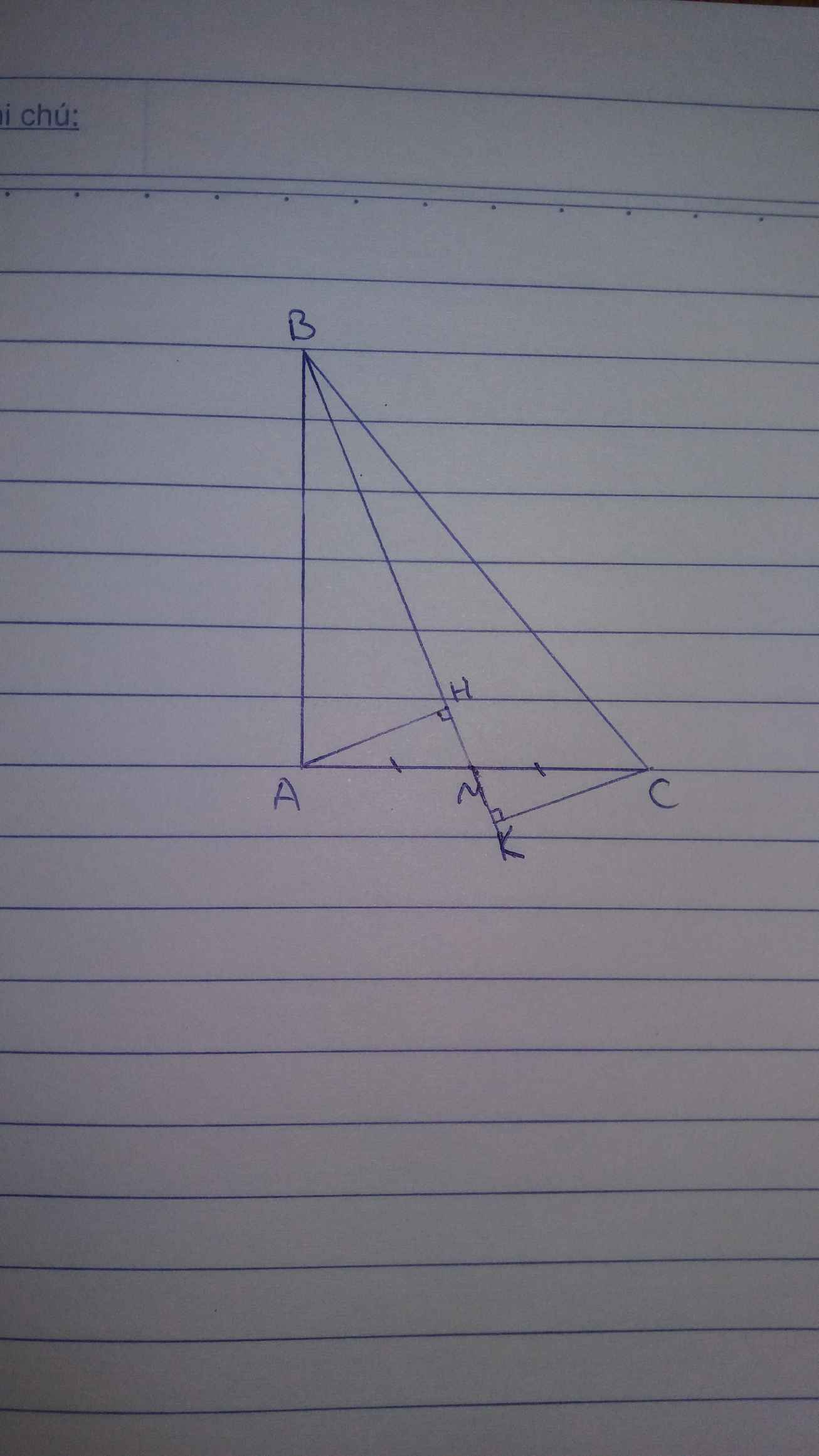

 giúp mình với ạ,mình xin cảm ơn trước
giúp mình với ạ,mình xin cảm ơn trước

\(\dfrac{3a+b+c}{a}=\dfrac{a+3b+c}{b}=\dfrac{a+b+3c}{c}\)
Áp dụng t/c DTSBN, ta có:
\(=\dfrac{3a+b+c+a+3b+c+a+b+3c}{a+b+c}=\dfrac{5\left(a+b+c\right)}{a+b+c}=5\)
\(\Rightarrow\dfrac{3a+b+c}{a}-3=\dfrac{a+3b+c}{b}-3=\dfrac{a+b+3c}{c}-3\)
\(=\dfrac{b+c}{a}=\dfrac{a+c}{b}=\dfrac{a+b}{c}=2\\ \Rightarrow\left\{{}\begin{matrix}2a=b+c\\2b=a+c\\2c=a+b\end{matrix}\right.\Leftrightarrow a=b=c\)
\(N=\dfrac{\left(a+a+a\right)^3}{a.a.a}=\dfrac{\left(3a\right)^3}{a^3}=\dfrac{27a^3}{a^3}=27\)