K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
PA
11 tháng 1 2019
tiếc quá chị ơi , em cũng muốn tìm người bạn. nhưng em mới lớp 7 thôi. hay chị em mình làm bạn nhé.
LN
1
8 tháng 7 2023
1: Khi x=64 thì A=7/(8+8)=7/16
2: =(x+3căn x+2căn x-24)/(x-9)=(x+5căn x-24)/(x-9)
\(=\dfrac{\left(\sqrt{x}+8\right)\left(\sqrt{x}-3\right)}{x-9}=\dfrac{\sqrt{x}+8}{\sqrt{x}+3}\)
17 tháng 8 2015
Lời giải đã được đăng ở đấy, post lại ở đây cho bạn dễ tìm
Để giải bài toán này đầu tiên ta có một nhận xét: Với mọi số dương \(x>0\) thì \(2x^3\ge3x^2-1.\) Thực vậy xét hiệu hai vế ta có \(2x^3-3x^2+1=\left(x-1\right)^2\left(2x+1\right)\ge0.\)
Bây giờ, gọi \(D,E,F\) là chân các đường cao kẻ từ \(A,B,C\). Theo hệ thức lượng trong tam giác vuông (liên hệ giữa cạnh và hình chiếu) ta có: Đối với tam giác vuông \(\Delta A'BC\) và đường cao \(A'D\) thì \(\frac{A'B^2}{A'C^2}=\frac{DB}{DC}\). Tương tự ta cũng có \(\frac{B'C^2}{B'A^2}=\frac{EC}{EA},\frac{C'A^2}{C'B^2}=\frac{FA}{FB}.\) Suy ra \(\frac{A'B^2}{A'C^2}+\frac{B'C^2}{B'A^2}+\frac{C'A^2}{C'B^2}=\frac{DB}{DC}+\frac{EC}{EA}+\frac{FA}{FB}\)
Vì ba đường cao đồng quy nên theo định lý Ceva \(\frac{DB}{DC}\cdot\frac{EC}{EA}\cdot\frac{FA}{FB}=1\). Do đó theo bất đẳng thức Cô-Si ta được
\(\frac{DB}{DC}+\frac{EC}{EA}+\frac{FA}{FB}\ge3\sqrt[3]{\frac{DB}{DC}\cdot\frac{EC}{EA}\cdot\frac{FA}{FB}}=3.\) Vì vậy mà \(\frac{A'B^2}{A'C^2}+\frac{B'C^2}{B'A^2}+\frac{C'A^2}{C'B^2}\ge3.\)
Từ đó áp dụng Nhận xét ta thu được \(2\left(\frac{A'B^3}{A'C^3}+\frac{B'C^3}{B'A^3}+\frac{C'A^3}{C'B^3}\right)\ge3\left(\frac{A'B^2}{A'C^2}+\frac{B'C^2}{B'A^2}+\frac{C'A^2}{C'B^2}\right)-3\ge3\cdot3-3=6.\)
Vì vậy ta được \(\frac{A'B^3}{A'C^3}+\frac{B'C^3}{B'A^3}+\frac{C'A^3}{C'B^3}\ge3.\)
Dấu bằng xảy ra khi và chỉ khi D,E,F là trung điểm ba cạnh AB,BC,CA và điều đó có nghĩa là tam giác ABC đều.
Nhớ thanks nhé!
HT
Ai giỏi toán giúp mình câu này với
giải phương trình: \(\left(2x^2-6x+5\right)\left(2x-3\right)^2=1\)
6
31 tháng 12 2018
\(\left(2x^2-6x+5\right)\left(2x-3\right)^2=1\)
\(\Leftrightarrow\left[2\left(2x^2-6x+5\right)\right].\left(2x-3\right)^2=2.1\)
\(\Leftrightarrow\left(4x^2-12x+10\right)\left(2x-3\right)^2=2\)
\(\Leftrightarrow\left[\left(2x\right)^2-2.2x.3+3^2+1\right]\left(2x-3\right)^2=2\)
\(\Leftrightarrow\left[\left(2x-3\right)^2+1\right]\left(2x-3\right)^2=2\) (1)
Đặt \(\left(2x-3\right)^2=c\left(c\ge0\right)\)
Suy ra (1) trở thành: \(c\left(c+1\right)=2\)
\(\Leftrightarrow\left(c-1\right)\left(c+2\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}c-1=0\\c+2=0\end{cases}\Leftrightarrow\orbr{\begin{cases}c=1\\c=-2\end{cases}}}\)
Vì \(c\ge1\) nên c = 1
Hay \(\Rightarrow\left(2x-3\right)^2=1\)
\(\Rightarrow\orbr{\begin{cases}2x-3=1\\2x-3=-1\end{cases}\Leftrightarrow\orbr{\begin{cases}x=2\\x=1\end{cases}}}\)
Vậy phương trình có hai nghiệm là x = 1 hoặc x = 2
P/s: Bài giải có nhiều sai sót, chị xem lại giúp em.
T
31 tháng 12 2018
P/s: Chữ (h) nghĩa là "hoặc"
\(\left(2x^2-6x+5\right)\left(2x-3\right)^2=1\)
Do 1 là số dương nên \(\left(2x^2-6x+5\right)\) và \(\left(2x-3\right)^2\) đồng dấu.
Mà \(\left(2x-3\right)^2\ge0\forall x\) nên chỉ cần xét 1 trường hợp:
\(\hept{\begin{cases}2x^2-6x+5=1\\\left(2x-3\right)^2=1\end{cases}}\Leftrightarrow\hept{\begin{cases}2x^2-6x+4=0\\2x-3=1..\left(h\right)..2x-3=-1\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}2\left(x-2\right)\left(x-1\right)=0\\2x=4...\left(h\right)...2x=2\end{cases}}\Leftrightarrow x=2...\left(h\right)...x=1\)
Vậy x = 2 hoặc x = 1
HM
19 tháng 1 2016
Câu hỏi tương tự nha bạn
Mình thấy Cô Loan Quản Lý giải bài đó
Tick mình nha Bạn ^_^
1 tháng 8 2018
Gọi T, V, A lần lượt là hs gỏi Toán, Văn, Anh
A)Hs giỏi 3 môn: T giao V giao A= ( T giao V) + ( V giao A) + ( T giao A) - 11 tất cả chia cho 3= (8+5+7-11)/3 = 3 (hs)
B) Hs giỏi đúng 1 môn Văn: 14-8- 2= 4( hs)( vì trong 5 hs vừa giỏi Văn, Anh đã có trong 3 hs giỏi 3 môn nên ta lấy 5-3=2)
Hs giỏi đúng 1 môn Toán : 15-8-4=3(hs) ( tương tự 7-3=4)
Hs giỏi đúng 1 môn Anh: 12-5-4= 3 (hs) ( tương tự 7-3=4)
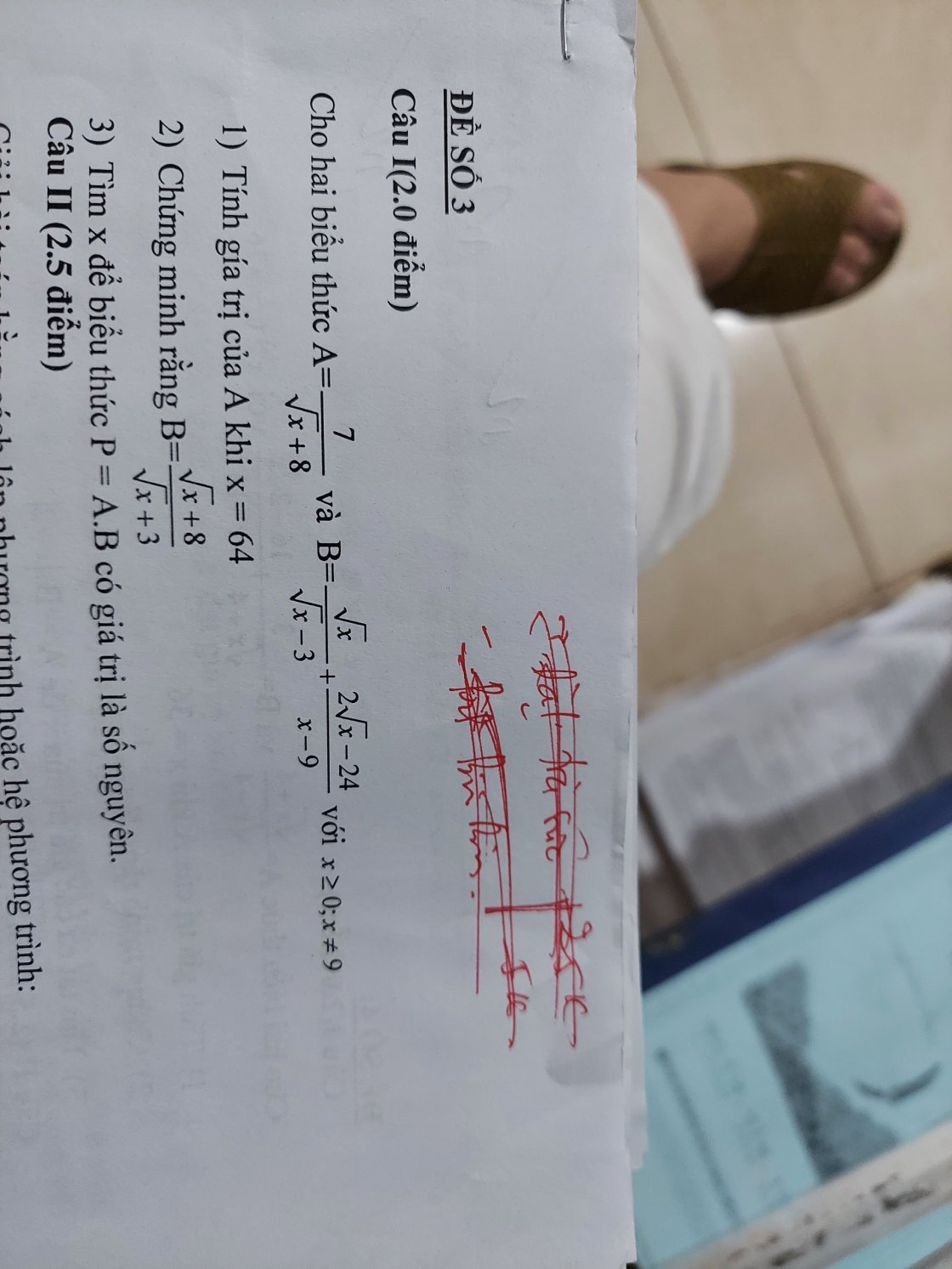
ko có ai có thể giúp bn học giỏi toán một cách diệu kì cả
chỉ có khi bạn thực sự nỗ lực hết mình và ôn luyện ngày đêm
mọi thứ sẽ thay đổi , thế nên từ bây h hãy vì việc học tập mà vươn lên bn nhé !!