
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Câu 14)
\(a,\\ =-\dfrac{3}{8}+\dfrac{8}{17}+\dfrac{-5}{8}-\dfrac{3}{5}+\dfrac{9}{17}\\ =\left(\dfrac{-3}{8}+\dfrac{-5}{8}\right)+\left(\dfrac{8}{17}+\dfrac{9}{17}\right)-\dfrac{3}{5}\\ =\left(-1\right)+1-\dfrac{3}{5}=0-\dfrac{3}{5}=\dfrac{-3}{5}\\ b,\\ =\dfrac{7}{15}.\dfrac{-15}{14}+\left(\dfrac{27}{16}-\dfrac{1}{8}\right):\dfrac{5}{8}\)
\(=\dfrac{-1}{2}+\dfrac{25}{16}.\dfrac{8}{5}=\dfrac{-1}{2}+\dfrac{5}{2}=2\\ c,\\ =\dfrac{2}{2}-\dfrac{2}{3}+\dfrac{2}{3}-\dfrac{2}{4}+.....+\dfrac{2}{99}-\dfrac{2}{100}\\ =1-\dfrac{1}{50}=\dfrac{49}{50}\)
Câu 15
\(a,2x+\dfrac{-1}{4}=\dfrac{3}{2}\\ 2x=\dfrac{3}{2}-\dfrac{-1}{4}=\dfrac{7}{4}\\ x=\dfrac{7}{4}:2=\dfrac{7}{8}\\ b,\dfrac{15}{x}=\dfrac{-3}{4}\\ x=\dfrac{15.4}{-3}=-20\)

Phân số chỉ 4m:
\(1-\left(\dfrac{7}{9}+\dfrac{1}{6}\right)=\dfrac{1}{18}\) (tấm vải)
Tấm vải dài:
\(4:\dfrac{1}{18}=72\left(m\right)\)
4m chiếm:
\(1-\left(\dfrac{7}{9}+\dfrac{1}{6}\right)=\dfrac{1}{18}\)(tấm vải)
Tấm vải dài số mét là:
\(4.18=72\left(m\right)\)
Đáp số: \(72m\)

a)\(123-5:\left(x+4\right)=38\)
\(5:\left(x+4\right)=123-38\)
\(5:\left(x+4\right)=85\)
\(x+4=5:85\)
\(x=\dfrac{1}{17}-4\)
\(x=-\dfrac{67}{17}\)
b)\(70-5.\left(x-3\right)=45\)
\(5.\left(x-3\right)=70-45\)
\(5.\left(x-3\right)=35\)
\(x-3=35:5\)
\(x-3=7\)
\(x=7+3\)
\(x=10\)

Gọi \(ƯC\left(12n+1;30n+2\right)=d\)
\(\Rightarrow12n+1⋮d\Rightarrow60n+5⋮d\)
và \(30n+2⋮d\Rightarrow60n+ 4⋮d\)
Do đó \(60n+5-60n-4⋮d\)
\(\Rightarrow1⋮d\)
\(\Rightarrow d=1\)
Vậy \(\dfrac{12n+1}{30n+2}\) là phân số tối giản.
Gọi (12n+1),(30n+2) là d (1)
=>30n+2 \(⋮\) d
=> 2(30n + 2) \(⋮\) d hay 60n +4 \(⋮\) d
Tương tự ta chưng minh:
12n + 1 \(⋮\)d (2)
=> 5(12n+1) \(⋮\) d hay 60n +5 \(⋮\)d
Do đó (60n + 5) - ( 60n +4 ) \(⋮\)d hay 1 \(⋮\) d
=> d = 1 hoặc -1
Từ (1) và(2) ta có( 12n+1 ;30n+2) =1
=> P/s 12n + 1 /30n+2 là ps tối giản

2a/3b = 3b/4c = 4c/5d = 5d/2a (1)
ta có: 2a/3b=3b/4c=> 8ac=9b^2
4c/5d=5d/2a=> 8ac=25d^2
=> 9b^2=25d^2
=> b=5d/3
=> 3b=5d(*)
lại có: 3b/4c=4c/5d => 3b/4c=4c/3b (theo *)
=> 9b^2=16c^2
=> b=4c/3
=> 3b/4c=1
BT= 4*3b/4c (Vì các phân số = nhau)
=> BT=3b/c
Mà: 3b=4c ( Vì 3b/4c=1)
=> BT=4c/c=4
Vậy biểu thức trên = 4


B5
a)\(A=\left(1-\dfrac{1}{2010}\right)\left(1-\dfrac{2}{2010}\right)\left(1-\dfrac{3}{2010}\right)\cdot...\cdot\left(1-\dfrac{2010}{2010}\right)\left(1-\dfrac{2011}{2010}\right)\\ =\left(1-\dfrac{1}{2010}\right)\left(1-\dfrac{2}{2010}\right)\left(1-\dfrac{3}{2010}\right)\cdot...\cdot\left(1-1\right)\left(1-\dfrac{2011}{2010}\right)\\ =\left(1-\dfrac{1}{2010}\right)\left(1-\dfrac{2}{2010}\right)\left(1-\dfrac{3}{2010}\right)\cdot...\cdot0\cdot\left(1-\dfrac{2011}{2010}\right)\\ =0\)
b)
\(A=\dfrac{1946}{1986}=\dfrac{1986-40}{1986}=\dfrac{1986}{1986}-\dfrac{40}{1986}=1-\dfrac{40}{1986}\\ B=\dfrac{1968}{2008}=\dfrac{2008-40}{2008}=\dfrac{2008}{2008}-\dfrac{40}{2008}=1-\dfrac{40}{2008}\)
Vì \(\dfrac{40}{1986}>\dfrac{40}{2008}\) nên \(1-\dfrac{40}{1986}< 1-\dfrac{40}{2008}\) hay \(A< B\)
B6
a) Đề sai
Sửa lại:
\(B=\dfrac{3}{1\cdot4}+\dfrac{3}{4\cdot7}+\dfrac{3}{7\cdot10}+...+\dfrac{3}{28\cdot31}\\ =\dfrac{1}{1}-\dfrac{1}{4}+\dfrac{1}{4}-\dfrac{1}{7}+\dfrac{1}{7}-\dfrac{1}{10}+...+\dfrac{1}{28}-\dfrac{1}{31}\\ =1-\dfrac{1}{31}\\ =\dfrac{30}{31}\)
b)
\(B=\dfrac{1}{2^2}+\dfrac{1}{3^2}+\dfrac{1}{4^2}+\dfrac{1}{5^2}+\dfrac{1}{6^2}+\dfrac{1}{7^2}+\dfrac{1}{8^2}\)
Ta thấy:
\(\dfrac{1}{2^2}< \dfrac{1}{1\cdot2}=\dfrac{1}{1}-\dfrac{1}{2}\)
\(\dfrac{1}{3^2}< \dfrac{1}{2\cdot3}=\dfrac{1}{2}-\dfrac{1}{3}\)
\(\dfrac{1}{4^2}< \dfrac{1}{3\cdot4}=\dfrac{1}{3}-\dfrac{1}{4}\)
...
\(\dfrac{1}{8^2}< \dfrac{1}{7\cdot8}=\dfrac{1}{7}-\dfrac{1}{8}\)
\(\Rightarrow B< \dfrac{1}{1}-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{4}+...+\dfrac{1}{7}-\dfrac{1}{8}\\ B< 1-\dfrac{1}{8}\\ B< \dfrac{7}{8}\left(1\right)\)
Mà \(\dfrac{7}{8}< 1\left(2\right)\)
Từ (1) và (2) ta có \(B< 1\)
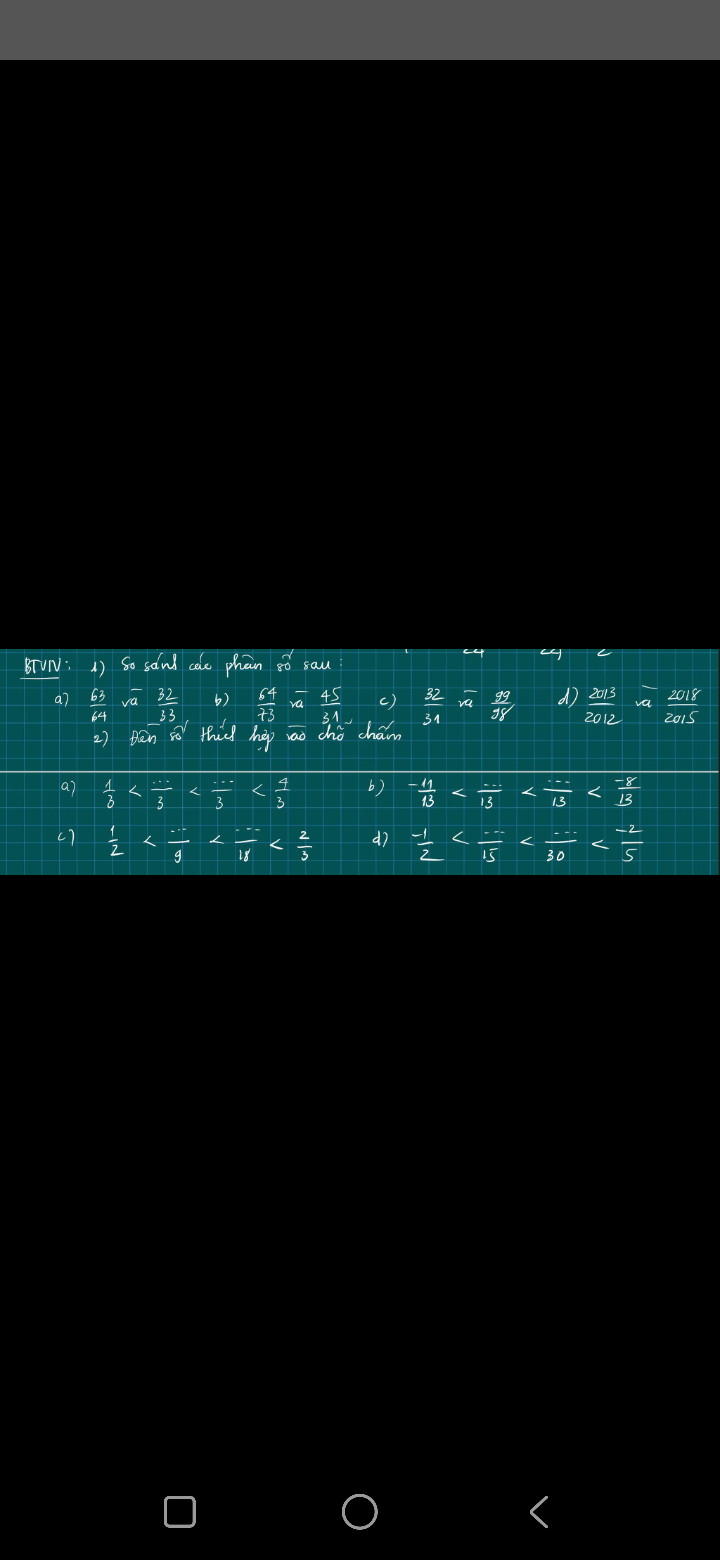


 giúp mk giải bài 5 vs bài 6 vs!!!!!!!!!!!!!!!!!!!
giúp mk giải bài 5 vs bài 6 vs!!!!!!!!!!!!!!!!!!!
c: Gọi hai số cần tìm là x,y
Theo đề, ta có: \(9< 2x< y< 12\)
=>2x=10 và y=11
=>x=5 và y=11
d: Gọi hai số cần tìm là x,y
Theo đề, ta có: \(-15< 2x< y< -12\)
=>2x=-14 và y=-13
=>x=-7 và y=-13